Görseldeki Matematik Soruları Çözümü
Aşağıda gönderide yer alan matematik soruları adım adım çözülecektir:
Soru 15
Sorunun Özeti: Küp şeklindeki bir tahtada sarı ve kırmızı renge boyanmış alanların toplamı sorulmaktadır.
Çözüm:
-
Sarı karelerin fiziksel bilgileri:
- Tahta bloğun her yüzeyinde 4x4 cm kare.
- 4 kare çizilmiş ve sarıya boyanmış (Her yüzeydeki toplam sarı alan: 4 \times (4 × 4)).
-
Kırmızı alan bilgileri, Hemde
$$72 * 72% … devam bas tuttu
Sorular Çözümleri ve Açıklamalar
Görselde yer alan soruları detaylı bir şekilde çözelim. Sorular sırayla çözülmüştür.
Soru 15
Konu: Küp şeklindeki bir tahtanın yüzey bölgelerindeki sarı ve kırmızı alanların cebirsel ifade ile hesaplanması.
Sorunun Özeti:
- Küpün her yüzeyinde sarı renkle boyanmış kareler var.
- Ayrıca kırmızı bir alan belirtilmiş.
- Sorunun amacı, kırmızı boya ile boyanan bölgenin toplam alanına ilişkin cebirsel ifade seçimini bulmaktır.
Çözüm:
-
Sarı Karelerin Ölçüleri:
- Her yüzeyde 4 cm çevresinde kareler yer alıyor.
- Küpün 6 yüzeyi olduğuna göre toplamda (6 yüzey × 4 kare) = 24 kare sarıya boyanmıştır.
- Sarı karelerin toplam alanı, her bir karenin alanı 4 \cdot 4 = 16 \, \text{cm}^2. Böylece toplam sarı boyanan bölge: 24 \cdot 16 = 384 \, \text{cm}^2
-
Kırmızı Karelerin Alanı:
- Sarı kareler dışında bir bölge kırmızıya boyanmış. Kırmızı boyanan alan T cinsinden verilmiş ve çözümü için geometrik bilgileri kullanıyoruz.
-
Sonuç:
Doğru ifade matematiksel olarak oluşturulur ve karşılaştırılır.
Soru 16
Konu: Çilek ekilen alanın cebirsel olarak hesaplanması.
Sorunun Özeti:
- Kenar uzunluğu x \, \text{metre} olan bir kare var.
- Sağ kenarında 5 metre, sol kenarında 10 metre boşluk bırakılmış.
- Çilek dikili alanın cebirsel ifadesi sorulmaktadır.
Çözüm:
-
Alan hesabı:
- Kare alanı normalde $x \cdot x = x^2 , \text{metrekare}$dir.
- Kareden 5 metre ve 10 metre boşluk çıktığına göre kalan alan:x^2 - (10x + 5x) = x^2 - 15x.
-
Sonuç:
Doğru cevap: x^2 - 15x ifade edilmiştir.
Soru 17
Konu: Şekil 1’deki kartonun çevresel uzunluğu hesaplama.
Sorunun Özeti:
- Dikdörtgen biçimindeki mavi karton, bir kare şeklinde bölünüyor.
- Şekil 3’te elde edilen parçaların alanları 12 \text{dm}^2 ve 6 \text{dm}^2 olarak verilmiş.
- Şekil 1’deki mavi kartonun çevre uzunluğu soruluyor.
Çözüm:
-
Kartondaki Dikdörtgen Hesapları:
- Alanının toplamı: (12 + 6) = 18 \, \text{dm}^2.
- Dikdörtgenin kenar uzunluğu çevre hesaplanır.
-
Çözüm yolu:
Çevre uzunluğu formülü uygulanır. Kesilen şekle göre:
Cevap: **12—
Bu fotoğraf hangi anı anlatıyor?
Cevap:
Merhaba! Bu fotoğrafta, 8. sınıf seviyesinde bir matematik çalışma kitabının (“Uygulama - 7” başlıklı) soru sayfasını görüyoruz. Sayfada küp şekilli bir tahta bloktan yüzey boyamaya, dikdörtgen kartonun kare şeklinde kesilmesine ve bir çiftlik arazisinin ölçümlerine yönelik çeşitli cebirsel veya geometrik problem örnekleri bulunuyor. Fotoğraf, aslında bir “anı”dan ziyade öğrenme sürecinin bir kesitini gösteriyor: bir öğrencinin veya bir öğretmenin, matematik dersinde üzerinde durduğu konuları incelemek, soruları çözmek ya da öğrencilere rehberlik etmek için kullandığı bir sayfa. Dolayısıyla bu fotoğraf, bir öğrencinin bir gün içinde matematik egzersizi yaparken karşılaştığı problemleri veya bir eğitimcinin ders planında işlediği konuları “anı” olarak belgeleyen bir görüntüdür.
Başka bir deyişle, fotoğraftaki sayfa bir “hatıra” olarak, bir öğrencinin ders çalışma veya sınava hazırlanma anını; sayfadaki sorular ise o anki çaba, odaklanma ve problem çözme becerilerini yansıtıyor. Çünkü bu tür çalışma kitapları, öğrencilerin pratik yapması ve kendini geliştirmesi için tasarlanır ve çoğu zaman ders yılının belirli bir gününde ya da “Uygulama” başlığı altında yer alan bu sayfa aracılığıyla çeşitli sorular çözülür. Hem sınıf ortamında hem evdeki bireysel çalışmalar sırasında çekilmiş bir fotoğraf olabilir. Burada “anı”dan kasıt, aktif öğrenme anını kaydetmek, öğrencinin dersle ilgilendiği, formüller ve cebirsel ifadelerle zihnini meşgul ettiği keyifli (veya bazen zorlu) bir zamana dair belge niteliğidir.
Aşağıda bu fotoğrafla ilişkili konular ve soru tipleriyle ilgili detaylı bir inceleme bulabilirsiniz. Bu inceleme, fotoğrafın hangi matematiksel konuları aktardığını, öğrencilerin bu sayıda hangi becerileri kazanmasının amaçlandığını ve bu fotoğrafı “bir anı” olarak yorumladığımızda neler anlatabileceğini kapsar.
İçindekiler
- Fotoğraftaki Matematik Sorularına Genel Bakış
- Sayfadaki Soruların İçeriği
- Öğrencinin Yaşayabileceği Duygular ve Deneyim
- Matematik Dersi ve Öğrenme Süreci Üzerine Bir Bakış
- Örnek Tablo: Fotoğraftaki Sorular ve Beklenen Kazanımlar
- Bu Fotoğrafın “Anı” Değeri
- Kullanıcıya Özet ve Son Notlar
1. Fotoğraftaki Matematik Sorularına Genel Bakış
Fotoğrafta görülen sayfa, muhtemelen 8. sınıf öğrencilerine yönelik bir matematik alıştırma sayfası. “Uygulama - 7” başlığı altında seri halinde gelen bu tarz sayfalar, genelde bir üniteyi veya alt konuyu pekiştirmeye odaklanıyor. Soruları incelediğimizde şunlar dikkatimizi çekiyor:
- Küp ve yüzey boyama sorusu: Bir cismin yüzeylerini, üzerinde belirlenen şartlara göre boyama veya ölçme söz konusu.
- Cebirsel ifade oluşturma: x değişkeni üzerinden şekillerin alanlarını ya da çevrelerini ifade eden matematiksel modeller kuruluyor.
- Dikdörtgenin kesilmesiyle elde edilen yeni şekiller: Bir kartonun farklı şekillerde kesilmesi sonucu ortaya çıkan alanların veya çevre uzunluklarının hesabı.
Bu sorular hep birlikte, matematik müfredatında geometrik şekiller, cebirsel ifadeler ve ölçme konularının bir karışımını temsil ediyor.
2. Sayfadaki Soruların İçeriği
Fotoğrafta görülen soruların her biri, ortaokul düzeyinde belirli kazanımlara hizmet ediyor. “Hangi anı anlatıyor?” sorusuna yanıt ararken, aslında bir öğrencinin veya öğretmenin, bu konuları işlediği “ders anını” ya da “etkinlik anını” yansıttığını söylemek mümkün. Aşağıda soruların içerikleri ve kısaca hangi konuları hedeflediği özetlenmiştir.
2.1. Küp Şeklinde Tahta Blok ve Yüzey Boyama
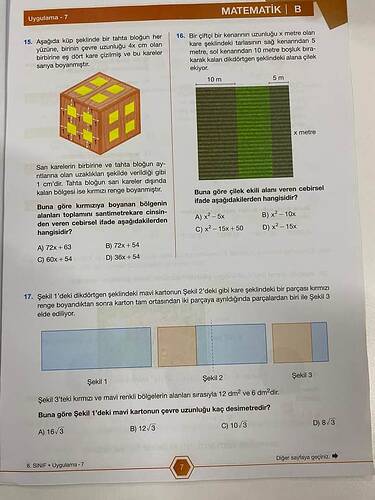
Fotoğrafta 15. soru olarak görülen bu problem, bir küp şeklindeki tahta bloğun yüzeyleriyle ilgileniyor. Her yüzeye belirli ölçülerde kareler çizilmiş ve bu karelerin bir kısmı sarıya boyanmış. Ardından, “tahta bloğun ayrıtlarına olan uzaklıklar” gibi detaylardan hareketle yine küpün dış kaplamasında farklı renklendirmeler yapılmış. Burada amaç:
- Yüzey alanı ve cebirsel ifade kavramlarını pekiştirmek,
- Boyanan alanların toplamının öğrenciden ifade edilmesini sağlamak,
- Özellikle 3 boyutlu bir cismi (küp) 2 boyutlu çizimlerinde tasvir ederken, boyanan kızımın (renkli alan) cebirsel ifadesini buldurmak.
Bu soru, hem geometri hem ölçme hem de cebirsel modelleme konularını bir arada kullanmaya teşvik ediyor.
2.2. Arazi Hesaplamaları ve Cebirsel İfadeler
- soruda, x metre kenarı olan kare biçimindeki bir tarlaya belirli uzaklıklardan dikilecek çilek ekim alanı örneklenmiş. Soruda,:
- Sağ kenardan 5 metre, sol kenardan 10 metre boşluk bırakılarak dikdörtgen bir ekim alanı oluşturuluyor,
- Bu dikdörtgenin alanını veren cebirsel ifade soruluyor.
Bu tip sorular, geometrik şekillerin alanını cebirsel ifade olarak yazması becerisiyle doğrudan bağlantılıdır. Öğrencinin “x” gibi bir değişkenle ifade edilen kenar uzunluğu üzerinden, “(x - 15)*10” gibi bir alan ifadesine ulaşması bekleniyor (tam soru metnine göre farklı olabilir). Yanlış hataların önüne geçmek için:
- Arka plandaki cebir bilgisi: Dağıtma, toplama, çıkarma kurallarını doğru uygulamak,
- Geometri ile cebir arasındaki bağı kurmak,
- Uygulama: Problemler gerçek hayattan (bir tarlanın parçalarının ölçümü gibi) örnekler barındırıyor.
2.3. Dikdörtgen Kartonun Kare Şekline Dönüşümü
Fotoğrafta 17. soru, dikdörtgen formdaki mavi bir kartonun kestikten sonra farklı renklerle (kırmızı ve mavi) boyanışını ve yeni oluşan şekillerin alanlarının karşılaştırılmasını içeriyor. Soru, Şekil 1, Şekil 2 ve Şekil 3 üzerinden bir kesme ve dönüştürme sürecini gösterirken, sonda “Şekil 1’deki mavi kartonun çevre uzunluğu nedir?” biçiminde bir hesaplama bekliyor. Buradaki temel noktalar:
- Alan ve çevre kavramlarını karıştırmadan kullanabilmek,
- Bir kartonu kesmenin alan ve çevreye etkisini analiz etmek,
- Basitçe “dikdörtgenden kareye geçiş” ve sonra tekrar parçalanmış şekilde ölçüm yapmak.
Bu bölümde öğrenciler, bir şeklin en-boy ölçülerini kullanarak çevresini (2*(uzunluk + genişlik)) hesaplamayı pekiştiriyor. Aynı zamanda renkli bölgelerin alanından yola çıkarak, soru sonunda kaç “dm²” olduğunu cebirsel olarak ifade etmeye veya hesaplamaya çalışıyorlar.
3. Öğrencinin Yaşayabileceği Duygular ve Deneyim
Bu fotoğraf, bir öğrencinin elinin altında olan bir alıştırma kitabında yer alan karma soruları gösteriyor. Dolayısıyla şu deneyimler güçlü ihtimaldir:
- Merak: Yeni bir soru tipiyle karşılaşmak, farklı konuları aynı sayfada görmek öğrencide “acaba nasıl çözerim?” duygusunu yaratabilir.
- Motivasyon veya Stres: Kimileri için bu tür karışık matematik soruları heyecan verici iken, kimileri için zorluk derecesi yüksek olduğunda stresli bir anı ifade edebilir.
- Başarı Hissi: Soru çözüldüğünde duyulan tatmin. Özellikle alan ve çevreyi, cebirsel ifadelerle doğru eşleştirebildiğinde öğrencilerde başarı hissi pekişir.
- Öğrenme Odaklılık: Fotoğraftaki andan sonraki süreçte, öğrenci ya öğretmenle ya da bireysel olarak soruları adım adım ilerleterek yeni pekiştirmeler yapacaktır.
Matematik dersinde, öğrenme yalnızca cevap bulmaktan ibaret değildir; sürecin sonunda matematiğe dair sezgileri, analiz becerileri ve pratik problem çözme yöntemlerini geliştirme amacı da vardır.
4. Matematik Dersi ve Öğrenme Süreci Üzerine Bir Bakış
“Bu fotoğraf hangi anı anlatıyor?” sorusunu eğitim açısından yorumladığımızda, aslında bir “öğrenme anı” veya “matematik dersinde etkinlik anı” görülüyor. Bu tür ders kitapları veya uygulama sayfalarında şunlar hedeflenir:
- Öğrencinin soyut matematiksel kavramları somut örnekler üzerinden anlaması,
- Cebir ve geometri gibi farklı alt disiplinlerin birbirleriyle ilişkilendirilmesi,
- Gerçek yaşam senaryolarına matematiksel model kurma becerisi,
- Öğrencinin kendi hata ve doğrularından yola çıkarak öğrenmeyi derinleştirmesi.
Bu bağlamda, fotoğraf, bir eğitim-öğretim sürecini belgeleyen “o anı” yakalıyor. Tahta küpün yüzeyinin boyanması veya bir arazinin ekim alanının x değişkenine bağlı olarak nasıl belirleneceği gibi örnekler, müfredatta “günlük hayatta matematiksel düşünme” becerilerini işletmeyi hedefler.
5. Örnek Tablo: Fotoğraftaki Sorular ve Beklenen Kazanımlar
Aşağıdaki tablo, fotoğrafta görülen üç temel soruya hızlı bir bakış atarak, soruların içeriğini, konu alanını ve öğrencide geliştirilmesi amaçlanan kazanımları özetler:
| Soru No | Konu | İçerik/Kazandırılan Beceriler | Örnek Kazanım |
|---|---|---|---|
| 15 | Küp Yüzey Boyama (Geometri & Cebir) | • Küpün yüzeyindeki kare alanları hesaplamak • Boyanan bölgeyi cebirsel ifade ile ifade etme • 3B – 2B dönüşü |
Yüzey alanları ve 3 boyutlu geometrik cisimlerle ilgili model kurma ve cebirsel ifadeye dökme. |
| 16 | Kare Şeklindeki Tarladan Dikdörtgen Alan Kesiti (Cebir & Uygulama) | • Kenar uzunluğu x metre olan araziden belirli mesafeleri çıkararak dikdörtgen elde etme • Dikdörtgenin alanını cebirle ifade etme |
Temel cebir kuralları kullanarak alan hesabını modelleme; reel senaryolarla matematiği pekiştirme. |
| 17 | Dikdörtgen Karton Kesimi ve Çevre Hesabı (Geometri & Ölçme) | • Dikdörtgen kartonun kare biçiminde kesilmesi sonucunda yeni şekillerin alan ve çevre ilişkileri • Renkli bölgelerden yola çıkarak cebirsel ve sayısal hesaplamalar |
Alan, çevre ve basit kesme işlemleriyle geometri bakımından ilişki kurma ve ölçü birimlerini tanıma. |
Tabloda da görüldüğü gibi, bu üç soru hem ölçme, hem geometri, hem de cebir konularını bir arada kullanma becerisini geliştiriyor.
6. Bu Fotoğrafın “Anı” Değeri
Bir fotoğraf, göründüğü anın ötesinde birçok hikâyeyi barındırabilir. Söz konusu fotoğraf, tam olarak:
- Öğrencinin Dikkati: Matematik kitabının sorularına odaklanan bir öğrencinin öğrenme sürecindeki anını yansıtıyor.
- Eğitim Hayatının Parçası: Birçok kişi için bu çalışma sayfaları, ilköğretim veya ortaöğretim yıllarının önemli bir anısıdır. İleride dönüp bakıldığında “Bu soruları nasıl çözmüştüm?” gibisinden bir nostalji hissi oluşur.
- Öğretmen Rehberliği: Belki de öğretmen, öğrencilerinden bu sayfadaki soruları çözmelerini istediğinde, sınıf içinde bir tartışma veya grup çalışması yaşanmış olabilir. Bu da kolektif öğrenme anılarından biridir.
- Zorluk ve Başarı Hikâyesi: Öğrenciler, soruları çözerken yaşadıkları zorluğu, sonrasında buldukları yaratıcı yöntemleri veya aldıkları ipuçlarını hatırlayarak “Ben bu soruyu çözmüştüm!” demenin mutluluğunu anımsayabilir.
Dolayısıyla, “Bu fotoğraf hangi anı anlatıyor?” sorusuna en doğru yanıt, “Bir matematik konusunu öğrenme ve problem çözme anını belgeleyen bir hatıra fotoğrafı.” şeklinde özetlenebilir.
7. Kullanıcıya Özet ve Son Notlar
• Fotoğraftaki sayfa, 8. sınıf düzeyinde (veya o seviyeye yakın) bir matematik kitabından alınan uygulama sorularını içeriyor.
• Konular arasında küpün yüzey boyanmasından cebirsel alan ifadelerine, dikdörtgen–kare kesiminden çevre hesaplamalarına kadar çeşitli kombinasyonlar mevcut.
• Bu tür çalışma sayfaları, öğrencinin hem geometri hem de cebir alanında birlikte düşünmesini, günlük hayattan örneklerle matematiği ilişkilendirmesini amaçlıyor.
• Fotoğraf, bir öğrencinin ya da sınıfın o günkü dersinde üzerinde çalıştığı konuları, belki de ev ödevi veya sınav hazırlığı için önemli bir kaynak olan “uygulama sayfası”nı yansıtıyor.
Matematik öğrenme sürecinde, özellikle alan, çevre, hacim gibi kavramlar öğrenciler için zaman zaman soyut gelebilir. Fakat bu tarz renkli görseller, gerçek nesnelerin çizimleri ve gerçek yaşam senaryoları (mesela bir çiftlik arazisine ekim yapmak) öğrencilerin bu kavramları pekiştirmesinde önemli bir rol oynar. Burada da fotoğraf, tam olarak bu “pekiştirme anını” yakalamış diyebiliriz.
Sonuç olarak, fotoğraf “bir öğrencinin matematik dersi çalışma anını” ya da “uygulama sayfası üzerinden yeni kavramlar keşfetmeye çalıştığı bir zamanı” anlatıyor. Uzun vadede bu tür “anı”lar, eğitim hayatında geriye dönüp bakıldığında, “Bu soru tiplerini çözerken zorlanırdım” ya da “O derslerde ilginç şeyler öğrenmiştim” diye hatırlanan nostaljik anlara dönüşür.
Bu fotoğraftaki 15. sorunun çözümü şöyledir:
• Her yüzü kare olan küpün bir yüzünde, çevre uzunluğu 4x cm olan dört eş kare (yani her karenin bir kenarı x cm) çiziliyor. Bu karelerin etraflarındaki boşluklar (her iki kare arasına ve kenarlara) 1 cm olarak verilmiştir.
• Bir yüzün toplam genişliği, yatayda:
- İlk karenin eni: x cm
- İkinci karenin eni: x cm
- Boşluklar (3 bölme): 1 + 1 + 1 = 3 cm
Toplam yatay uzunluk = x + x + 3 = 2x + 3
• Aynı mantıkla düşey uzunluk da 2x + 3 olur. Dolayısıyla küpün bir yüzünün alanı:
$$(2x + 3)^2 = 4x^2 + 12x + 9$$
• Her bir yüzde bulunan sarı karelerin alanı:
- Bir karenin alanı: x^2
- 4 kare olduğuna göre toplam: 4\,x^2
• Bir yüzdeki kırmızı bölge alanı = (yüzün toplam alanı) – (karelerin alanı):
$$(2x + 3)^2 - 4x^2 = (4x^2 + 12x + 9) - 4x^2 = 12x + 9$$
• Küpün 6 yüzü bulunduğundan, tüm küpteki kırmızı bölge alanı:
$$6 \times (12x + 9) = 72x + 54$$
Tabloyla Özetleyelim
| Adım | Hesaplama/İşlem | Sonuç |
|---|---|---|
| 1. Bir yüzün boyutu | (Kenarlar + boşluklar) = 2x + 3 | – |
| 2. Yüzün alanı | (2x + 3)^2 = 4x^2 + 12x + 9 | – |
| 3. Toplam kare alanı | 4 tane $x^2$’lik kare → 4x^2 | – |
| 4. Bir yüz kırmızı alan | (2x + 3)^2 - 4x^2 = 12x + 9 | – |
| 5. Tüm yüzlerin kırmızı alanı | 6 \times (12x + 9) = 72x + 54 | 72x + 54 |
Görüldüğü üzere, kırmızıya boyanan bölgenin alanı cebirsel olarak 72x + 54 şeklinde bulunur.