Bölme işlemi ödevi

İLKOKUL 4.sınıf
,
1

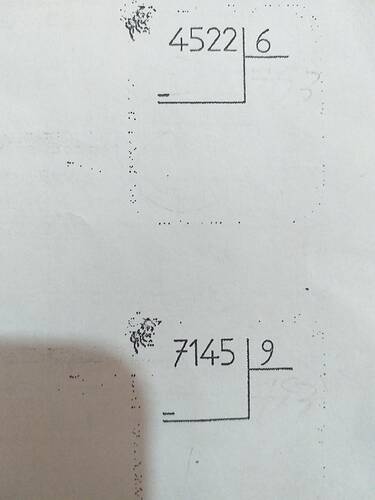
17354887435646148780834089341612
173548874356461487808340893416122448×3264 460 KB

2

Görüntüdeki Bölme İşlemleri Nasıl Yapılır?

Cevap:

Görsellerde iki farklı uzun bölme işlemi bulunmaktadır. Bunları sıra ile çözelim.

1. Bölme İşlemi: 4522 ÷ 6

Adım adım bölme işlemini yapalım:

  1. Çözüm Yöntemi:

    • İlk olarak, 4’ün içinde 6 kaç defa bulunur? Bu mümkün değil çünkü 4, 6’dan küçüktür. Bu durumda, 4 yerine iki basamağı alacağız: 45.
    • 45’in içinde 6 kaç defa bulunur? 7 defa (çünkü 6 * 7 = 42 ve 6 * 8 = 48, 48 fazla büyük).
    • 45’ten 42’yi çıkar. Sonuç: 3.
    • Şimdi 2’yi aşağıya indir, yanına: 32.
    • 32’nin içinde 6 kaç defa bulunur? 5 defa (çünkü 6 * 5 = 30 ve 6 * 6 = 36, fazla büyük).
    • 32’den 30’u çıkar. Sonuç: 2.
    • Şimdi son basamağı, 2’yi aşağıya indir, yanına: 22.
    • 22’nin içinde 6 kaç defa bulunur? 3 defa (çünkü 6 * 3 = 18 ve 6 * 4 = 24, fazla büyük).
    • 22’den 18’i çıkar, kalan: 4.

  2. Sonuç:

    • İşlem sonucu: 753, kalan: 4.

2. Bölme İşlemi: 7145 ÷ 9

Bu işlem de adım adım çözülebilir:

  1. Çözüm Yöntemi:

    • 7’nin içinde 9 kaç defa bulunur? Bu mümkün değil, iki basamak alın: 71.
    • 71’in içinde 9 kaç defa bulunur? 7 defa (çünkü 9 * 7 = 63 ve 9 * 8 = 72, fazla büyük).
    • 71’den 63’ü çıkar. Sonuç: 8.
    • 8’in yanına 4’ü indir: 84.
    • 84’ün içinde 9 kaç defa bulunur? 9 defa (çünkü 9 * 9 = 81 ve 9 * 10 = 90, fazla büyük).
    • 84’ten 81’i çıkar. Sonuç: 3.
    • 3’ün yanına 5’i indir: 35.
    • 35’in içinde 9 kaç defa bulunur? 3 defa (çünkü 9 * 3 = 27 ve 9 * 4 = 36, fazla büyük).
    • 35’ten 27’i çıkar, kalan: 8.

  2. Sonuç:

    • İşlem sonucu: 793, kalan: 8.

Sonuç:

  • 4522 ÷ 6 işleminin sonucu 753, kalan: 4.
  • 7145 ÷ 9 işleminin sonucu 793, kalan: 8.

Bu bölme işlemleri, uzun bölme yöntemi kullanılarak yapılmıştır. Uzun bölme, büyük sayıların bölünmesinde adım adım bir işlem süreci izlenmesini sağlar.