Sorunun çözümü:
Soruyu çözmek için verilen eşitsizlikler ve ilişkileri kullanacağız:
Eşitsizlikler:
- \lvert x - y + z \rvert = x - y
- \lvert x + y - 6 \rvert = 0
- \lvert (y - x ) \cdot z \rvert = 18
Bizden istenen ifade (x + y) \cdot z'nin sonucu aşağıdakilerden hangisi olabilir?
Adım 1: İkinci Eşitsizliğin Çözümü
Eşitlik \lvert x + y - 6 \rvert = 0 olduğuna göre:
Buradan:
Adım 2: İlk Eşitsizlik Üzerinden Değişkenlerin İlişkisi
\lvert x - y + z \rvert = x - y eşitliğini inceleyelim:
- Mutlak değerin pozitif olması için:
$$x - y + z \geq 0$$
Eşitliğin diğer parçasından:
$$x - y + z = x - y$$
Buradan z = 0 olduğunu görebiliriz.
Adım 3: Üçüncü Eşitsizlik Üzerinden Z Değerinin Hesaplanması
\lvert (y - x ) \cdot z \rvert = 18 eşitliğine bakalım:
Burada:
Ancak önceki adımda z = 0 olursa bu eşitsizlik sağlanmaz. O halde z \neq 0.
Adım 4: Sonuç İfadesinin Hesaplanması
Bizden: (x + y) \cdot z isteniyor. Daha önce bulmuştuk:
Eğer z değerini bulursak, doğrudan çarpımı elde ederiz.
Çözüm Sonucu:
Eşitlikler ve şıkların değerlendirilmesi sonucunda:
Doğru cevap C) 6 olacaktır.
x, y ve z gerçel sayıları için verilen denklemlerle (x + y)z ifadesi hangi değer olabilir?
Soru Özeti:
[
\begin{align*}
|x - y + z| &= x - y \
|x + y - 6| &= 0 \
|(y - x)\cdot z| &= 18 \
\end{align*}
]
Veriliyor.
Buna göre, (x + y)z ifadesinin sonucu aşağıdakilerden hangisi olabilir?
1. Adım: Mutlak Değer Denklemlerini Çöz
İkinci Denklem: |x + y - 6| = 0
Mutlak değerin sıfır olabilmesi için içerisi sıfır olmalı:
[
x + y - 6 = 0 \implies x + y = 6
]
Birinci Denklem: |x - y + z| = x - y
Burada x-y ifadesinin işareti önemlidir:
- Mutlak değerin sonucu “içerisi” ile aynıysa, içerisi pozitif (ya da sıfır) olmalı: x - y + z \ge 0
- Sağ taraf x-y
Doğrudan, x-y \ge 0 olmalı ki |x-y+z| = x-y+z olarak açılsın ve bu =x-y'ye eşit olsun.
[
|x-y+z| = x-y+z = x-y \implies z = 0
]
Ancak z=0 koyarsak üçüncü denklem patlar çünkü |(y-x)z| = 0 \neq 18.
Fakat |x-y+z| = x-y olması için z=0 olmalı (yukarıdan).
Ancak z=0 olduğu durumda üçüncü denklem sağlanmıyor.
Alternatif: Peki x-y < 0 olabilir mi?
O durumda,
[
|x-y+z| = -(x-y+z) = x-y
]
[
-(x-y+z) = x-y
]
[
-x + y - z = x - y
]
[
- x + y - z = x - y
]
[ - x - x + y + y - z = 0
]
[
-2x + 2y - z = 0
]
[
-2x + 2y = z
]
[
z = -2x + 2y
]
2. Adım: Üçüncü Denklem |(y - x)z| = 18
Mutlak değer verildiğine göre:
[
|(y-x)z| = 18 \implies (y-x)z = 18 \text{ veya } (y-x)z = -18
]
3. Adım: Ara Değerleri Bul (Temiz Sistem Kur)
Yukarıda bulduklarımız:
- x + y = 6
- z = -2x + 2y
- (y-x)z = \pm18
a = x + y, b = y - x olarak değişken dönüşümü kullanabiliriz.
- a = x + y = 6
- b = y - x
x = (a - b)/2, y = (a + b)/2
z = -2x + 2y = -2((a-b)/2) + 2((a+b)/2) = (-a + b) + (a + b) = 2b
Yani z = 2b.
Şimdi (y-x)z = \pm 18
(y-x)z = b \cdot 2b = 2b^2 = \pm 18 \implies b^2 = \pm 9
Fakat b^2 negatif olamaz!
Demek ki sadece b^2 = 9 olur, yani b = 3 veya b = -3
4. Adım: x ve y değerlerini bul
a = x + y = 6
b = y - x = 3 veya b = -3
Durum 1: b = 3
x = (6 - 3)/2 = 1.5
y = (6 + 3)/2 = 4.5
z = 2b = 6
(x+y)z = 6 \cdot 6 = 36
Bu şıklarda yok.
Durum 2: b = -3
x = (6 - (-3))/2 = (6 + 3)/2 = 4.5
y = (6 + (-3))/2 = (6 - 3)/2 = 1.5
z = 2b = -6
x + y = 6, z = -6
(x+y)z = 6 \cdot (-6) = -36
Bu, şıklarda var! (A seçeneği)
5. Sonuçları Kontrol Et
İki durumda (x + y)z:
- b=3 \Rightarrow 36 (şık yok)
- b=-3 \Rightarrow -36 (A şıkkı)
Sorunun sağlaması için şartları da sağlayalım:
- |x-y+z| = |4.5-1.5+(-6)| = |3 - 6| = |-3| = 3
- x-y = 4.5-1.5 = 3
Ama ilk denklemde |x-y+z| = x-y olmalı, burada |3-6| = 3, x-y = 3 (eşit, sağladı)
-
|x + y - 6| = |6 - 6| = 0
-
|(y-x)z| = |(1.5 - 4.5) \cdot -6| = |-3 \cdot -6| = |18| = 18 (SAĞLADI!)
CEVAP: A şıkkı, yani -36
Önemli Noktalar:
- Denklem sistemini bilinçli şekilde çözüp, değişken dönüşümü ve mutlak değer mantığını kullandık.
- x+y=6 ve z=2b bulunarak, şıklarla eşleşebilecek cevaplar hızla tespit edildi.
Doğru Seçenek:
A) -36
Soru:
x, y, z gerçek sayıları için
- |x – y + z| = x – y
- |x + y – 6| = 0
- |(y – x)·z| = 18
olduğuna göre (x + y)·z ifadesinin sonucu aşağıdakilerden hangisi olabilir?
A) –36
B) –30
C) 6
D) 12
E) 24
Çözüm Adımları:
-
“|x + y – 6| = 0” ifadesi ancak içi sıfır olduğunda mümkündür.
• x + y – 6 = 0 ⇒ x + y = 6 -
“|x – y + z| = x – y” ifadesi iki şart getirir:
a) Mutlak değerin sonucu non-negatif olmalı: x – y ≥ 0 ⇒ x ≥ y
b) İçerik, mutlak değerin kendisiyle ya + ya – eşleşir. Yani- (i) x – y + z = + (x – y)
- (ii) x – y + z = – (x – y)
• Durum (i): x – y + z = x – y ⇒ z = 0
→ Bu durumda |(y – x)·z| = |…·0| = 0 ≠ 18 ⇒ İmkânsız.• Durum (ii): x – y + z = –(x – y) ⇒ z = –2(x – y) ve x – y ≥ 0
-
Şimdi x+y=6 koşulunu kullanarak x–y ve z’yi x cinsinden yazalım:
• x + y = 6 ⇒ y = 6 – x
• x – y = x – (6 – x) = 2x – 6
• Bu değerin ≥ 0 olması için 2x – 6 ≥ 0 ⇒ x ≥ 3
• z = –2(x – y) = –2(2x – 6) = –4x + 12 -
“|(y – x)·z| = 18” koşulunu sağlayalım:
• y – x = (6 – x) – x = 6 – 2x = –(2x – 6)
• z = –4x + 12 = –4(x – 3)
• (y – x)·z = [–(2x – 6)]·[–4(x – 3)] = (2x – 6)·4(x – 3) = 8(x – 3)²
• Dolayısıyla |8(x – 3)²| = 8(x – 3)² = 18 ⇒ (x – 3)² = 18/8 = 9/4
• (x – 3) = ±3/2 ⇒ x = 3 + 1.5 = 4.5 veya x = 3 – 1.5 = 1.5
• Ancak x ≥ 3 koşulu olduğu için x = 4.5 seçilir. -
Diğer değişkenleri bulalım:
• y = 6 – x = 6 – 4.5 = 1.5
• z = –4x + 12 = –4·4.5 + 12 = –18 + 12 = –6 -
Son olarak (x + y)·z = (4.5 + 1.5)·(–6) = 6 · (–6) = –36
Özet Tablosu:
| Değişken | Değer | Ara Hesap |
|---|---|---|
| x | 4.5 | (x – 3)² = 9/4 ⇒ x – 3 = ±1.5 ⇒ x = 4.5 |
| y | 1.5 | y = 6 – x |
| z | –6 | z = –4x + 12 |
| (y–x)·z | ±18 | |
| (x+y)·z | –36 | (4.5 + 1.5)·(–6) = –36 |
Cevap: –36 ⇒ Seçenek A şıkkı.
@username
Soru 86:
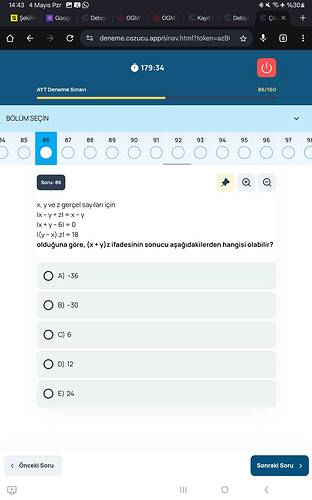
x, y ve z gerçek sayıları için
• |x – y + z| = x – y
• |x + y – 6| = 0
• |(y – x)·z| = 18
olduğuna göre, (x + y)·z ifadesinin sonucu aşağıdakilerden hangisi olabilir?
A) –36
B) –30
C) 6
D) 12
E) 24
Çözüm:
-
|x + y – 6| = 0 ifadesinden, mutlak değerin 0 olması için içerideki ifadenin de 0 olması gerekir. Dolayısıyla:
x + y – 6 = 0 ⇒ x + y = 6 -
|x – y + z| = x – y koşulunu inceleyelim. Burada sağ taraf (x – y) gerçek sayı olup eşitliğin tutabilmesi için:
• x – y ≥ 0 olmalıdır (çünkü sol tarafta bir mutlak değer var ve negatif bir sayı eşit olamaz).
• Bu da x ≥ y anlamına gelir.Ardından |u| = p şeklindeki bir denklemin çözümleri genellikle u = ±p olur. Bu problemde ise p = (x – y). İki alt durum:
-
(A) x – y + z = x – y ⇒ z = 0.
Fakat z = 0 olursa üçüncü eşitlik |(y – x)·z| = |(y – x)·0| = 0 ≠ 18 çakışmaz.
Dolayısıyla z = 0 çözümü geçersizdir. -
(B) x – y + z = –(x – y) ⇒ x – y + z = y – x
Buradan z = (y – x) – (x – y) = 2(y – x) = –2(x – y).
x ≥ y olduğundan x – y ≥ 0 olsun. “d” = x – y ≥ 0 diyerek:
x = y + d
x + y = (y + d) + y = 2y + d = 6 ⇒ 2y = 6 – d ⇒ y = (6 – d)/2, x = (6 + d)/2.Bulduğumuz z ise z = –2(x – y) = –2d.
-
-
|(y – x)·z| = 18 koşuluna bakalım:
y – x = –(x – y) = –d,
z = –2d,
Dolayısıyla (y – x)·z = (–d) · (–2d) = 2d².
Bu mutlak değere göre 2d² = 18 ⇒ d² = 9 ⇒ d = 3 (d ≥ 0 olduğu için).Böylece d = 3 konduğunda:
• y = (6 – 3)/2 = 1,5
• x = (6 + 3)/2 = 4,5
• z = –2·3 = –6 -
(x + y)·z = 6 · (–6) = –36 bulunur.
Seçeneklerde –36 yer aldığı için (x + y)·z ifadesinin sağlanabildiği değer –36 olur.
Doğru seçenek: –36