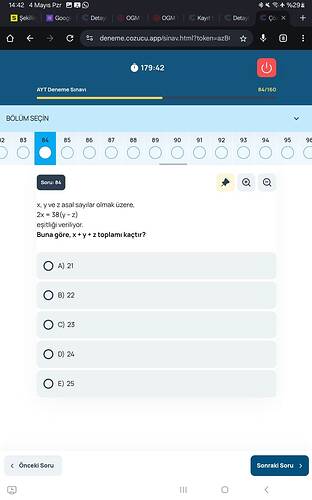
Çözüm: x, y ve z asal sayılar olmak üzere, 2x = 38 (y − z), x + y + z toplamı nedir?
Soruyu çözmek için verilen eşitliği kullanacağız:
Denklem:
Bu eşitliği asal sayı olan x, y ve z değerlerini bulmak için parçalayacağız.
Adım 1: Denklemden y – z’yi bulmak
Denklemi sadeleştirirsek:
Buradan anlıyoruz ki x, 19 ile bölündüğünde tam sayı (ve asal) olmalı.
Adım 2: Asal sayı olan x değeri
x asal sayı olacak şekilde 19’un katı olmalıdır. Bu durumda x = 19 olabilir (en küçük asal 19’dur).
Adım 3: y − z değerini hesaplamak
x = 19 iken:
Adım 4: y ve z asal sayılar
y ve z asal sayılar olacak şekilde ve farkları 1 olacak şekilde seçilmelidir. En küçük asal sayılar:
- y = 3
- z = 2
Bu değerler y − z = 3 − 2 = 1 eşitliği sağlar.
Adım 5: Toplamı hesaplama
Sonuç:
x + y + z toplamı = 24
Doğru seçenek: D) 24
x, y ve z asal sayılar olmak üzere, 2x = 38(y – z) eşitliği veriliyor. Buna göre x + y + z toplamı kaçtır?
Yanıt:
Sorunun Analizi ve Çözüm Yolu
Verilen denklem:
Her iki tarafı 2’ye bölelim:
Burada x, y, z asal sayılar ve y - z farkı da pozitif bir tam sayı olmalı (asal sayıların sıralamasına göre y > z).
x asal bir sayı, ve x = 19 × (y−z) olduğundan, x’in asal olması için (y−z) = 1 olmalıdır; çünkü 19’dan başka asal bir çarpan olamaz.
Çünkü:
- Eğer y − z = 1 ise, x = 19 × 1 = 19 (asal).
- y − z = 1 dışında başka bir değer alırsa, x asal olmaz (çünkü asal çarpanın katı olur).
- y = z + 1, yani iki asal sayı arka arkaya olmalı.
Ardışık asal sayılar şunlardır:
- 2 ve 3
- 3 ve 5
- 5 ve 7
- 11 ve 13
- 17 ve 19
Burada dikkat: y ve z’nin ardışık asal sayılar olmasını sağlarsak x de asal (19) olur.
Şimdi x = 19 kesinleşti.
Ayrıca y − z = 1 → y = z + 1
Şimdi asal ardışık çiftler bakıyoruz. Fakat y = z + 1 için mevcut asal çiftler sadece (2, 3) için vardır. Ancak 19 en büyük asal, o yüzden uygun ardışık asalları bulalım:
- y = 3, z = 2 (x = 19 için, y > z olmalı!)
- y = 19, z = 18 (Fakat z asal olmaz)
- y = 13, z = 12 (z asal değil)
- y = 7, z = 6 (z asal değil)
- y = 3, z = 2 (z ve y asal!)
Şimdi bu durumda:
- x = 19
- y = 3
- z = 2
Ve x, y, z hepsi asal.
Şimdi toplam:
Sonuç ve Cevap
- Doğru cevap: D) 24
- x = 19, y = 3, z = 2 asal sayıları ile eşitlik sağlanmaktadır.
- Kontrol: 2x = 2 × 19 = 38, y–z = 3–2 = 1, 38×1=38’de sağlanır.
Kısa Özet ve Anahtar Noktalar
- x = 19, y = 3, z = 2 asal sayıları seçildi.
- Cevap: 24
x, y ve z asal sayılar olmak üzere, 2x = 38(y - z) eşitliği veriliyor. Buna göre x + y + z toplamı kaçtır?
Answer:
2x = 38(y - z) ifadesini sadeleştirelim:
2x = 38(y - z)
x = 19(y - z)
x asal sayıdır. 19 da asal bir sayıdır. 19(y - z)’nin asal olması için (y - z) = 1 olmalıdır; aksi takdirde 19’la çarpımı bileşik sayı olur.
Dolayısıyla:
y - z = 1
y ve z de asal sayılar olduğuna göre ve aralarındaki fark 1 olduğunda tek ihtimal (y, z) = (3, 2)’dir (çünkü 3 ve 2 tek farkla asal olan en küçük-tek çiftidir).
Bu durumda:
x = 19 · (3 - 2) = 19
y = 3
z = 2
x + y + z = 19 + 3 + 2 = 24
Doğru seçenek, (D) 24’tür.
Soru (84):
x, y ve z asal sayılar olmak üzere
[
2x = 38,(y - z)
]
eşitliği veriliyor. Buna göre (x + y + z) toplamı kaçtır?
Çözüm Adımları:
-
Denklemi sadeleştirelim:
[
2x = 38(y - z)
\quad\Longrightarrow\quad
x = 19,(y - z).
] -
Sağ tarafta (19) asal çarpanı var. (x) de asal olduğuna göre çarpımın
- ya bir çarpanı 1,
- ya da bir çarpanı (\pm1) olmalıdır (negatif asal tanım dışında kaldığından biz pozitif farkı düşünürüz).
Bu durumda tek makul seçenek:
[
y - z = 1
\quad\text{ve}\quad
x = 19\cdot1 = 19.
] -
Yine (y) ve (z) birbirinden 1 farkla ayrılan asal sayı olmalı. Pozitif farklı ve ardışık asallar yalnızca
[
z = 2,\quad y = 3
]
durumu sağlar. -
Sonuç olarak
[
x = 19,\quad y = 3,\quad z = 2
]
ve bunların toplamı
[
x + y + z = 19 + 3 + 2 = 24.
]
Cevap: 24 (D şıkkı)