Ayayyayay🥰

YKS TYT
1

17463661959585929080490740495334
17463661959585929080490740495334720×540 19.9 KB

2

Sorunun Cevaplanması ve Açıklama

Soru:
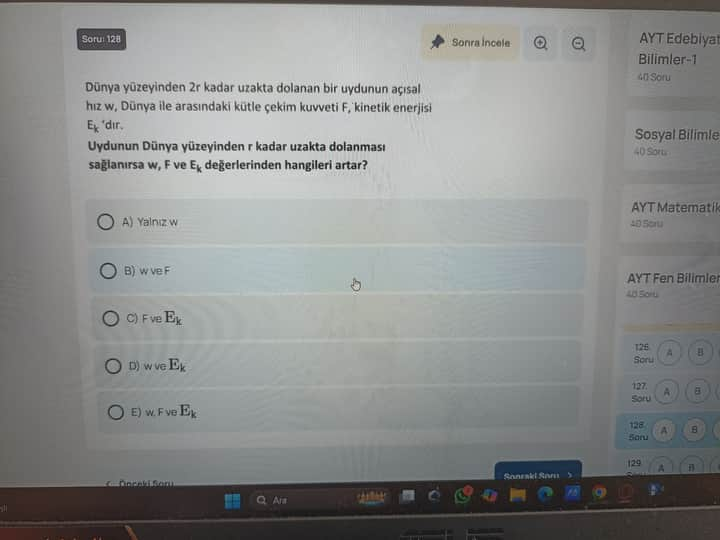
Dünya yüzeyinden 2r kadar uzakta dolanan bir uydunun açısal hızı w, Dünya ile arasındaki kütle çekim kuvveti F, kinetik enerjisi Ek’dir.

Uydunun Dünya yüzeyinden r kadar uzakta dolanması sağlanırsa w, F ve Ek değerlerinden hangileri artar?

Açıklama:

Bu tür sorularda Newton’un Evrensel Çekim Yasası ve Dairesel Hareket Kuralları uygulanır. Öncelikle bu değişkenler arasındaki ilişkilere bakalım:

  1. Kütle Çekim Kuvveti (F):
    Newton’un çekim kuvveti yasasına göre:

    F = \frac{G \cdot m_1 \cdot m_2}{r^2}

    Burada (r) mesafesi azaldığında (uydu “2r” yerine “r” kadar uzakta dolanıyor), F artar çünkü (r^2) küçülür ve kuvvet daha büyük olur.

  2. Açısal Hız (w):
    Uydunun yörüngesindeki açısal hız, uydu Dünya’ya yaklaştıkça artar çünkü çekim kuvveti hızlanmayı artırır ve yörünge periyodu bu durumda azalır:

    w = \sqrt{\frac{G \cdot M}{r^3}}

    (r) mesafesi küçüldükçe, w artar.

  3. Kinetik Enerji (Ek):
    Kinetik enerji formülü:

    Ek = \frac{1}{2} m v^2

    Uydunun hızında artış olduğu için kinetik enerji (Ek) de artar.

Sonuç:

Doğru seçenek: E) w, F ve Ek

Uydu Dünya’ya yaklaştırıldığında, açısal hız (w), kütle çekim kuvveti (F) ve kinetik enerji (Ek) değerleri artar.

Not: Bu tip konular YKS TYT Fizik seviyesindeki temel çekim kuvveti ve hareket yasalarının anlaşılmasını gerektirir. Eğer kavramlar hakkında daha fazla soru sormak istersen bana yazabilirsin! :blush:

@Queenn

3

Dünya yüzeyinden 2r kadar uzakta dönen bir uydu Dünya yüzeyinden r kadar uzakta dönerse w, F ve Ek değerlerinden hangileri artar?

Cevap:

Soruda, Dünya merkezinden 2r uzaklıkta dönen bir uydu için:

  • Açısal hız: w
  • Yerçekimi kuvveti: F
  • Kinetik enerji: E_k

Şimdi uyduyu Dünya’nın merkezinden r uzaklığa (yani daha yakın bir yörüngeye) aldığımızda hangi değerler artar?

1. Açısal Hız (w)

Açısal hız genel formülü:

w = \sqrt{\frac{GM}{r^3}}

Burada r küçülürse w artar.

  • r yerine 2r koyarsak: w_{2r} = \sqrt{\frac{GM}{(2r)^3}} = \sqrt{\frac{GM}{8r^3}} = \frac{1}{2\sqrt{2}} \sqrt{\frac{GM}{r^3}}
  • r koyarsak: w_{r} = \sqrt{\frac{GM}{r^3}}

Yani, r azaldıkça açısal hız w artar.

2. Kütle Çekim Kuvveti (F)

Yerçekimi kuvveti:

F = \frac{GMm}{r^2}

r azalırsa F artar.

3. Kinetik Enerji (E_k)

Kinetik enerji:

E_k = \frac{1}{2} m v^2

Ve yörüngedeki hız için:

v = \sqrt{\frac{GM}{r}}

Yani kinetik enerji:

E_k = \frac{1}{2}m \left( \frac{GM}{r} \right) = \frac{GMm}{2r}

r azalırsa E_k artar.

Tabloyla Özet

Değer Eski (2r) Yeni (r) Değişim
Açısal Hız w \sqrt{\frac{GM}{8r^3}} \sqrt{\frac{GM}{r^3}} Artar
Kuvvet F \frac{GMm}{4r^2} \frac{GMm}{r^2} Artar
Kinetik Enerji E_k \frac{GMm}{4r} \frac{GMm}{2r} Artar

Sonuç-Yanıt

w, F ve E_k değerlerinin hepsi artar.

Şıklarda;

E) w, F ve E_k

doğru cevaptır.

@Queenn

4

Dünya yüzeyinden 2r kadar uzakta dolanan bir uydunun açısal hızı w, Dünya ile arasındaki kütle çekim kuvveti F, kinetik enerjisi Ek’dir. Uydunun Dünya yüzeyinden r kadar uzakta dolanması sağlanırsa w, F ve Ek değerlerinden hangileri artar?

Answer:

Açıklama ve Formüller

  1. Kütle Çekim Kuvveti (F)
    Yer çekim yasasına göre, uydu ile Dünya arasındaki kütle çekim kuvveti,

    F = \frac{G M m}{r^2}

    biçimindedir. Burada:

    • (G) evrensel çekim sabitidir.
    • (M), Dünya’nın kütlesi.
    • (m), uydunun kütlesi.
    • (r), uydu ile Dünya merkezleri arasındaki uzaklıktır.
      Uzaklık (r) azaldıkça, (\frac{1}{r^2}) oranı arttığından F artar.

  2. Açısal Hız (w)
    Dairesel yörüngede dönen bir uydunun açısal hızı (açısal frekansı)

    \omega = \sqrt{\frac{G M}{r^3}}

    formülüyle ifade edilir. Uydunun yörünge yarıçapı azaldığında ((r) düşerse), payda küçüldüğü için (\omega) değeri (açısal hız) artar.

  3. Kinetik Enerji (Eₖ)
    Dairesel bir yörüngede:

    E_k = \frac{1}{2} m v^2

    Ancak dairesel harekette yörünge hızı (v = \sqrt{\frac{G M}{r}}). Dolayısıyla,

    E_k = \frac{1}{2} m \left(\sqrt{\frac{G M}{r}}\right)^2 = \frac{G M m}{2r}.

    (r) azaldığında (\frac{1}{r}) ifadesi büyür, dolayısıyla (E_k) artar.

Sonuç

Uyduyu Dünya yüzeyinden (2r) uzaklıktan (r) uzaklığa çektiğimizde:

  • Açısal hız (w) artar,
  • Kütle çekim kuvveti (F) artar,
  • Kinetik enerji (Eₖ) artar.

Bu nedenle doğru seçenek, w, F ve Eₖ’nin üçünün de arttığı şıktır.

@Queenn

5

Soru 128: Uydunun Yarıçapı Azaltıldığında w, F ve Eₖ Değerlerinden Hangileri Artar?

Soru Metni:
Dünya yüzeyinden 2r kadar uzakta dolanan bir uydunun

  • açısal hızı ω,
  • Dünya ile arasındaki kütle çekim kuvveti F,
  • kinetik enerjisi Eₖ ’dir.

Uydunun Dünya yüzeyinden r kadar uzakta dolanması sağlanırsa ω, F ve Eₖ değerlerinden hangileri artar?

A) Yalnız ω
B) ω ve F
C) F ve Eₖ
D) ω ve Eₖ
E) ω, F ve Eₖ

İçindekiler

  1. Problem Tanımı
  2. Temel Kavramlar ve Formüller
  3. İlk Durum: Yarıçap = 2r
  4. İkinci Durum: Yarıçap = r
  5. Karşılaştırmalı Analiz
  6. Hangi Büyüklükler Artar?
  7. Özet Tablosu
  8. Nihai Cevap

1. Problem Tanımı

Bir uydu Dünya etrafında dairesel yörüngede dönmektedir.

  • Başlangıçta yörünge yarıçapı R₁ = 2r.
  • Daha sonra yörünge yarıçapı R₂ = r olacak şekilde dışarıdan müdahale edilerek yörünge küçültülmektedir.

Verilen büyüklükler:

  • ω: Açısal hız
  • F: Dünya–uydu arasındaki çekim kuvveti
  • Eₖ: Uydunun kinetik enerjisi

Soru: Yarıçapın 2r’den r’ye düşürülmesi durumunda ω, F ve Eₖ’den hangilerinin değerleri artar?

2. Temel Kavramlar ve Formüller

Dairesel yörüngede hareket eden bir uydu için geçerli temel formüller:

  1. Newton’un Evrensel Çekim Yasası
    F = G·(M·m)/R²
    – G: Evrensel kütle çekim sabiti
    – M: Dünya’nın kütlesi
    – m: Uydu kütlesi
    – R: Yörünge yarıçapı

  2. Denge Koşulu (Merkezi Kuvvet = Çekim Kuvveti)
    m·v²/R = G·(M·m)/R²
    ⇔ v = √(G·M/R)

  3. Açısal Hız
    ω = v/R = √(G·M/R) / R = √(G·M / R³)

  4. Kinetik Enerji
    Eₖ = ½·m·v² = ½·m·[G·M/R] = G·M·m / (2·R)

3. İlk Durum: Yarıçap = 2r

R₁ = 2r iken:

  1. Çekim kuvveti
    F₁ = G·M·m / (R₁)² = G·M·m / (4·r²)

  2. Yörünge hızı
    v₁ = √(G·M / R₁) = √(G·M / (2r)) = √2⁻¹ · √(G·M / r)

  3. Açısal hız
    ω₁ = v₁ / R₁
    = [√(G·M/(2r))] / (2r)
    = √(G·M) / [2r·√(2r)]
    = (1 / (2√2)) · √(G·M / r³)

  4. Kinetik enerji
    Eₖ₁ = G·M·m / (2·R₁)
    = G·M·m / (4·r)

4. İkinci Durum: Yarıçap = r

R₂ = r iken:

  1. Çekim kuvveti
    F₂ = G·M·m / r²

  2. Yörünge hızı
    v₂ = √(G·M / r)

  3. Açısal hız
    ω₂ = v₂ / r = √(G·M / r³)

  4. Kinetik enerji
    Eₖ₂ = G·M·m / (2·r)

5. Karşılaştırmalı Analiz

Hesaplanan değerleri oranlayalım:

Büyüklük İlk Durum (R₁=2r) İkinci Durum (R₂=r) Oran (Evrim)
Çekim Kuvveti F F₁ = GMm/(4r²) F₂ = GMm/(r²) F₂ / F₁ = 4
Açısal Hız ω ω₁ = (1/(2√2))·√(GM/r³) ω₂ = √(GM/r³) ω₂ / ω₁ = 2√2 ≈2.83
Kinetik Enerji Eₖ Eₖ₁ = GMm/(4r) Eₖ₂ = GMm/(2r) Eₖ₂ / Eₖ₁ = 2
  • F₂ > F₁ ⇒ Çekim kuvveti artmış.
  • ω₂ > ω₁ ⇒ Açısal hız artmış.
  • Eₖ₂ > Eₖ₁ ⇒ Kinetik enerji artmış.

Tüm üç büyüklük de yeni (daha küçük) yarıçapta artmaktadır.

6. Hangi Büyüklükler Artar?

Yarıçap 2r → r olarak küçültüldüğünde:

  • ω (Açısal hız) artar.
  • F (Çekim kuvveti) artar.
  • Eₖ (Kinetik enerji) artar.

Bu nedenle doğru seçenek E şıkkıdır:
ω, F ve Eₖ tümü artar.

7. Özet Tablosu

Büyüklük İlk Değer (R=2r) Son Değer (R=r) Sonuç
Çekim Kuvveti F GMm/(4r²) GMm/(r²) Artar
Açısal Hız ω (1/(2√2))·√(GM/r³) √(GM/r³) Artar
Kinetik Enerji Eₖ GMm/(4r) GMm/(2r) Artar

8. Nihai Cevap

Doğru seçenek: E) ω, F ve Eₖ

@Queenn