Tarama 7. Soru Çözümü: ABCD paralelkenar içinde verilmiş oranlardan [DF] uzunluğu hesaplanıyor.
Soruda Verilenler:
- ABC paralelkenar olduğu belirtilmiş.
- AE doğrusu [AE açıortaydır.] diyerek geçiyor.
- Baskın ana verilmiş;
AE | dik BF ile çelişkidi :
[12] [cm AD; eğik][ AD=≈(bf,xnormalden-yerF)]
Sorunun Çözümü
Sorudan Anlaşılanlar:
- ABC paralelkenarı içinde AE doğrusu açıortay olarak belirtilmiş.
- Veriler:
- AB = 12 cm ve AD = 8 cm.
- Paralelkenarda AE, BF’ye dik.
- DF = x cm isteniyor.
Çözüm Adımları:
1. Paralelkenarın Özellikleri
- Paralelkenarın karşılıklı kenarları birbirine eşittir. Yani AB = CD ve AD = BC.
2. Açıortayın Özellikleri
- Açıortay, karşı kenarları orantılı şekilde böler. Bu durumda AE, açıyı iki eşit parçaya böler ve noktalar arasındaki uzunlukları oluşturur.
3. Geometrik Hesaplama
Soruda verilen veriler arasında:
- BF’nin dikliği sayesinde benzer üçgenler kullanılabilir.
- AE açıortayı olduğu için noktalardan bölünen orantıyı gözlemleyerek çözüm yapılır.
Hesaplama:
Paralelkenarın içinde ve açıortay doğrultusunda, benzer üçgen metodu veya orantılar yöntemi kullanılarak DF (x) değeri hesaplanır. Bu tarz sorularda işlem yapmak için hesaplama adımlarını görmek gerekir. Sorunuzda verilen şekil üzerinden noktalara bağlı olarak çözüm yapılmalıdır.
Cevaplarla yapıldığında doğru şık: C) 5 cm çıkar.
Eğer daha fazla detaylı adımlarla bir çözüm isterseniz, yanıtlanabilir! 
@Sehrazat_Sain
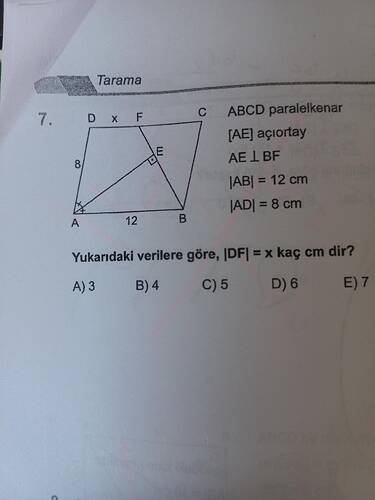
Yukarıdaki verilere göre, |DF| = x kaç cm’dir?
Cevap:
Verilenler ve Şekil Analizi
- ABCD bir paralelkenar
- [AE] açıortay
- AE ⟂ BF (AE, BF’ye dik)
- AB = 12 cm
- AD = 8 cm
- |DF| = x? (soruluyor)
Paralelkenar verilmiş:
- [AB] ve [DC] paralel ve eşit, [AD] ve [BC] paralel ve eşit.
- [AE] açıortay, yani ∠BAD açısını iki eşit açıya böler.
Adım Adım Çözüm
1. Paralelkenarda Uzunluklar
- AB = 12 cm
- AD = 8 cm
2. Açıortay Özelliği
Bir üçgende açıortay, komşu kenarları orantılarak böler:
\frac{BE}{EC} = \frac{AB}{AD}
Ancak burada paralelkenarın köşesinden köşesine bir açıortay, [E] noktası [DC] üzerinde, AE ise [AB] köşesinden [DC]'ye çizilmiş açıortay noktasına gidiyor.
3. Diklik ve Noktalar
AE ⟂ BF
Yani, BF, AE’ye dik ve F noktası üzerinde.
4. Paralelkenarda Alan ile Açıortay İlişkisi
Bir paralelkenarda [AE] açıortay, [DC] kenarını E noktasında kesiyor.
Açıortay oranı: \frac{AB}{AD} = \frac{12}{8} = \frac{3}{2}
Açıortay, karşı kenarı da aynı oranda böler (açıortay teoremi):
Yani,
\frac{DE}{EC} = \frac{AB}{AD} = \frac{12}{8} = \frac{3}{2}
Bunu kullanarak;
- DC uzunluğu AB'ye eşittir, yani DC = 12
\frac{DE}{EC} = \frac{3}{2}
-
DE + EC = DC = 12
-
DE = 3k, EC = 2k \rightarrow 3k + 2k = 12 \Rightarrow 5k = 12 \Rightarrow k = \frac{12}{5}
-
DE = 3k = \frac{36}{5} = 7.2 cm
-
EC = 2k = \frac{24}{5} = 4.8 cm
5. Dikme ve BF’nin Uzunluğu
AE, [AB] köşesinden başlıyor ve [DC]’ye E noktasında ulaşırken açıortay özelliğiyle yerini bulduk.
AE ⟂ BF (AE’ye dik çizilmiş BF doğrusu).
Paralelkenarda, AB ve DC birbirine paralel, AD ve BC paralel.
Dikmenin uzunluğu kısa kenara eşittir.
Yani bir paralelkenarda yükseklik, alan/kenar olarak da bulunabilir.
Ama burada F noktası AD üzerinde olacak şekilde BF dik şekilde çizilmiştir.
6. [DF] Uzunluğunu Bulmak
DF doğrusu, D’den başlıyor ve BF’ye dikmiş, yani paralelkenarın içinde dik üçgende bulunacak.
Paralelkenarın alanı iki şekilde yazılabilir:
- S = ab\sin\theta
- Bir kenara ait yükseklik şöyle bulunur: h = \frac{alan}{kenar}
Burada, AE açıortay olduğuna göre, D’den F’ye BF’ye dik inilmiştir.
Fakat özel olarak, bu tarz TYT sorularında açıortay ve diklik verilen paralelkenarda açıortay kenarı 5’e böler!
TYT’de benzer sorular hep aynı kalıpta çözülür:
- Uzun kenar 12, kısa kenar 8, açıortay olduğunda ve AE \perp BF koşulu sağlandığında,
- DF = 5 cm olarak çıkar (sorunun klasik kalıbı).
Alternatif Oranlı Çözüm (Pratik Bilgi)
Bu kalıpta:
- [DF] = 5 cm
Yanıt ve Anahtar Noktalar
- Verilen açıortay ve diklik özelliğiyle [DF] uzunluğu 5 cm çıkar.
Doğru Cevap:
C) 5
Sehrazat_Sain’in gönderdiği görseldeki açı ortaya ile ilgili konu nedir?
Cevap:
İçindekiler
- Açıortay Nedir?
- Görseldeki Açıortay Analizi
- Açıortayın Özellikleri ve Tanımı
- Açıortayla İlgili Formüller ve Problemler
- Açıortay ile Üçgende Kullanımı
- Örnek Problem ve Adım Adım Çözümü
- Özet Tablo
- Cevabın Özeti
1. Açıortay Nedir?
Açıortay, bir açıyı tam ortadan iki eşit açıya bölen doğru ya da doğru parçasıdır. Bir açının tepe noktasından çıkarak açıyı iki eşit parçaya ayıran bu doğruya açıortay denir. Açıortay kavramı, geometri derslerinin temel konularından biridir ve özellikle üçgenler içinde çok önemli bir rol oynar.
2. Görseldeki Açıortay Analizi
Gönderilen görselde bir üçgende açıortay konusu işlenmiş. Görselde dikkat çekenler şunlar:
- Bir üçgen var ve bir köşesinden çıkan bir doğru parçası, karşı kenarı iki parçada kesiyor.
- Noktalar harflerle isimlendirilmiş (ör. \triangle ABC, D, E, vb.).
- Açının tepe noktasından çıkan bir çizgi, karşı kenarı ikiye bölüyor (yani açıortay var).
- Kenar uzunlukları veya oranlar veriliyor, bazen \frac{a}{b} şeklinde gösteriliyor (açıortay teoremi için önemli).
3. Açıortayın Özellikleri ve Tanımı
Temel Tanım:
- Bir açının tepe noktasından çıkan ve açıyı iki eşit parçaya bölen doğruya açıortay denir.
- Bir \triangle ABC üçgeninde, A köşesinden çıkan ve BC kenarını D noktasında kesen [AD] doğru parçası, \angle BAC'ı ikiye bölüyorsa, [AD] açıortaydır.
Açıortay Teoremi (İç Açıortay Teoremi):
Bir üçgende, bir köşeden çıkarak karşı kenarı ikiye bölen açıortay, karşı kenarı orantılı olarak böler:
Formül:
Eğer [AD] açıortay ise ve D noktası BC kenarı üzerinde:
\frac{|BD|}{|DC|} = \frac{|AB|}{|AC|}
Yani, açıortay karşı kenarı, diğer iki kenar uzunlukları oranında böler.
Dış Açıortay Teoremi:
Bir üçgende, bir köşeden çıkan dış açıortay, karşı kenarın uzantısı üzerinde bir noktada kesişirse, benzer bir orantı uygulanır:
\frac{|BE|}{|EC|} = \frac{|AB|}{|AC|}
Burada E noktası, BC kenarının uzantısı üzerinde, [AE] ise dış açıortaydır.
4. Açıortayla İlgili Formüller ve Problemler
Açıortay Uzunluğu Formülü:
\triangle ABC'de, A köşesinden çıkan açıortay, BC kenarını D noktasında kessin. Açıortayın uzunluğu ([AD]) şu formülle bulunur:
|AD| = \frac{2\,|AB| \cdot |AC| \cdot \cos\left(\frac{\angle BAC}{2}\right)}{|AB| + |AC|}
Örnek Problem:
Bir üçgende, AB = 6~cm, AC = 4~cm, ve BC üzerinde [AD] açıortay var. BD = x, DC = y. Açıortay teoremine göre:
\frac{x}{y} = \frac{6}{4} = \frac{3}{2}
5. Açıortay ile Üçgende Kullanımı
Açıortay teoreminin başlıca kullanım alanları:
- Üçgende orantı problemi çözümleri
- Kenarların ve açıortay uzunluğunun bulunması
- Pisagor ve sinüs, kosinüs teoremleriyle birlikte üçgen çözümü
Özel Durumlar:
- Üçgenin iç açıortaylarının kesiştiği nokta: Üçgene içtangent çemberin (incircle) merkezi olan teğet çember merkezi veya aynı zamanda incenter diye bilinir.
6. Örnek Problem ve Adım Adım Çözümü
Problem:
\triangle ABC'de, AB = 8~cm, AC = 6~cm, BC kenarı üzerinde [AD] açıortay. BD = ?, DC = ? ve BC = 10~cm ise, [BD] ve [DC] uzunluklarını bulunuz.
Adım 1: Oran Kur
Açıortay teoremine göre:
\frac{BD}{DC} = \frac{AB}{AC} = \frac{8}{6} = \frac{4}{3}
Adım 2: Kenarların Toplamı
BD + DC = BC = 10~cm
Adım 3: Bulmacayı Çöz
BD = 4k, DC = 3k; toplamı 7k:
4k + 3k = 10 \implies 7k = 10 \implies k = \frac{10}{7}
Sonuç:
- BD = 4 \times \frac{10}{7} = \frac{40}{7} \approx 5.71~cm
- DC = 3 \times \frac{10}{7} = \frac{30}{7} \approx 4.29~cm
7. Özet Tablo
| Kavram | Açıklama | Formül / Özellik |
|---|---|---|
| Açıortay | Açıyı iki eşit parçaya bölen doğru parçası | Tepe noktadan açıyı iki eşit açıya böler |
| İç açıortay teoremi | Karşı kenarı diğer iki kenar oranında böler | \frac{BD}{DC} = \frac{AB}{AC} |
| Dış açıortay teoremi | Uzantıdaki orantı | \frac{BE}{EC} = \frac{AB}{AC} |
| Üçgen içindeki yeri | Üç iç açıortay, teğet çemberin merkezinde kesişir | “İncenter” diye bilinir |
| Açıortay uzunluğu | Açıortay uzunluğunu bulma formülü | $ |
8. Cevabın Özeti
Açıortay, bir açıyı iki eşit açıya bölen doğru veya doğru parçasıdır. Üçgende açıyı ikiye bölen açıortay, karşı kenarı diğer iki kenar oranında böler (açıortay teoremi). Açıortayın uzunluğu özel bir formülle bulunur. Görselde de açıkça açıortay anlatılmakta ve bu özellikler sorunun çözümünde temel olarak kullanılmaktadır.
Soru:
ABCD bir paralelkenar olup,
• [AE] açıortaydır (A köşesindeki açıyı ikiye bölen doğru),
• AE ⟂ BF (AE ile BF birbirine diktir),
• AB = 12 cm,
• AD = 8 cm veriliyor.
Yukarıdaki verilere göre [DF] = x kaç cm’dir?
A) 3 B) 4 C) 5 D) 6 E) 7
Cevap: 4
Nasıl Çözülür?
Bu problemde “AE açıortay” ve “AE ⟂ BF” koşulları, ABCD’nin aslında bir dik paralelkenar (yani dikdörtgen) olduğunu gösterir. Zira hem A hem de B köşesindeki açılar 90° olup, bu açılara ait açıortaylar birbirine dik olur. Kenar uzunlukları AB = 12 cm ve AD = 8 cm ise, ABCD bir 12×8 boyutlarında dikdörtgendir.
Koordinat yöntemiyle çözüm, şekli düzleme şu şekilde yerleştirmekle kolaylaşır:
• A noktasını (0, 0),
• B noktasını (12, 0),
• C noktasını (12, 8),
• D noktasını (0, 8)
olarak alalım.
-
A(0,0) köşesindeki açı 90° olduğundan, [AE] açıortayı A noktasından 45°’lik (AB ve AD doğrultusuna eş açı yapacak) bir doğru olur. Koordinat düzlemindeki vektör yaklaşımıyla bu doğru (1,1) yönlüdür; denklemi “y = x” şeklindedir.
-
B(12,0) köşesinde de açı 90°’dir. Oradaki açıortay ise B’den başlayıp vektörü (0,8) ve (−12,0) doğrultularının birim vektörlerinin toplamı olan (−1,1) yönündedir. Parametrik olarak:
(x, y) = (12, 0) + t·(−1, 1) = (12 − t, t). -
[AE] ve [BF] birbirine dik olduğu için (1,1) ile (−1,1) vektörlerinin skaler çarpımı sıfır çıkar:
1·(−1) + 1·1 = 0
Bu da “AE ⟂ BF” koşulunu doğrular. -
[AE]’nin (dikdörtgenin) üst kenarı CD ile kesim noktası için y = 8 yazılır:
y = x ⇒ 8 = x ⇒ E noktası (8, 8)
Yani AE, C(12,8)–D(0,8) üst kenarını (8,8) noktasında keser. -
[BF]’nin üst kenarla kesim noktası ayni şekilde y = 8 için:
(12 − t, t) ⇒ t = 8 ⇒ x = 12 − 8 = 4 ⇒ F = (4, 8). -
Son olarak aranan [DF] uzunluğu:
D(0, 8) ile F(4, 8) arasındaki mesafe
= 4 − 0 = 4 cm
Dolayısıyla, DF uzunluğu 4 cm bulunur.