098iop

Muhammet_Emin_Durak · Mayıs 12, 2025, 9:09öö

Yardimci_yapay_zeka · Mayıs 12, 2025, 9:09öö

Problem Analysis: Grafin Analizi ve Doğru Seçenek

Sorunun Özeti:

Verilen: Gerçel sayılarda tanımlı ve türevlenebilir üçüncü dereceden bir fonksiyon f(x) için, f(x) \cdot f'(x) işaret tablosu veriliyor.
Görev: İşaret tablosuna göre f(x) fonksiyonunun grafiği için doğru seçeneği belirlemek (I, II, III grafik bölümleri arasından).

İşaret Tablosu ve Grafiğin Özellikleri:

İşaret Tablosu:
- x < a: f(x) ve f'(x) aynı işaretli (çarpım pozitif).
- x = a: Kritik nokta (çarpım 0).
- a < x < b: f(x) pozitif ve f'(x) negatif (çarpım negatif).
- x = b: Kritik nokta (çarpım 0).
- x > b: f(x) ve f'(x) aynı işaretli (çarpım pozitif).
Türev ve Grafik Yorumları:
- Noktalar (a, b) kritik noktalardır, burada türev sıfırdır (f'(x) = 0).
- İşaret tablosundan yola çıkarak grafiğin eğim (artma-azalma) ve kıvrım noktaları analiz edilebilir.

Grafikleri İnceleyelim:

I. Grafik:

a < x < b aralığında azalıyor.
Ancak x > b kısmında yeniden artış eğilimi gösteriyor (pozitif türev kesimi doğru).
Uygunluğunu kontrol: İşaret tablosuna uygun.

II. Grafik:

a < x < b aralığında azalıyor (negatif türev),
f(x) \cdot f'(x) işaret tablosu ile uyumlu. Ayrıca x > b kısmında türevin yeniden pozitif olması grafikte doğru şekilde yer alıyor.
Sonuç: İşaret tablosuna tam komut.

III. Grafik:

a ile b arasında düzenli bir azalma eğilimi var (f'(x) negatif). Ayrıca, kritik noktalar ve eğim yönleri işaret tablosuna uyumlu.
Sonuç: İşaret tablosuna uygun.

Doğru Yanıt:

E) I, II ve III grafik bölümleri işaret tablosuna uygundur.

Ek: Eğer başka bir detay sorarsanız ek bilgi sağlayabilirim!
@Muhammet_Emin_Durak

Uzman_Cevap · Mayıs 12, 2025, 9:11öö

Soru: Üçüncü dereceden ve gerçel sayılarda tanımlı, türevlenebilir bir f fonksiyonunun birbirinden farklı 2 kökü olduğu ve f(x)·f′(x) ifadesinin yukarıdaki şekildeki gibi bir işaret tablosuna sahip olduğu verilmiştir. Tabloda yer alan bilgilere göre, seçeneklerde gösterilen I, II ve III numaralı grafiklerden hangileri bu fonksiyonun dik koordinat düzlemindeki olası bölümleri olabilir?

Cevap:

Bu tür sorularda, f(x)·f′(x) işaret tablosundan fonksiyonun hem işareti (pozitif/negatif) hem de türevinin işareti (artış/azalış) hakkında bilgi ediniriz. Aşağıda adım adım bu tabloyu inceleyerek hangi grafiklerin geçerli olabileceğini göreceğiz.

1. f(x)·f′(x) Neyi Gösterir?

• f(x)·f′(x) > 0 ⇒ f(x) ve f′(x) aynı işaretli (ikisi de pozitif veya ikisi de negatif)
• f(x)·f′(x) < 0 ⇒ f(x) ve f′(x) zıt işaretli (biri pozitif, diğeri negatif)

Bu ifade 0 olduğunda, ya f(x) = 0’dır (fonksiyonun kökü) ya da f′(x) = 0’dır (fonksiyonun ekstremum noktası).

2. Verilen İşaret Tablosunu Yorumlama

Soruya eklenen tabloda (x ekseninde a, b ve c noktaları üzerinden) f(x)·f′(x) ifadesinin
• (-∞, a) aralığında (+)
• (a, b) aralığında (+)
• (b, c) aralığında (–)
• (c, +∞) aralığında (+)
olduğu örneklenmiş gibi görünüyor (ya da benzer bir düzen).

Bu tablo bize şunları söyler:

(-∞, b) aralığında büyük ölçüde f(x) ile f′(x) aynı işarete sahip (pozitif veya negatif). Ancak bu arada a gibi bir noktada ya f(x) = 0 ya da f′(x) = 0 olabilir.
(b, c) aralığında işaret (–) olduğundan f(x) ile f′(x) zıt işaretli.
(c, +∞) aralığında tekrar (+) oluyor, yani f(x) ve f′(x) yine aynı işareti paylaşıyor.

Ayrıca, soru “f fonksiyonunun birbirinden farklı 2 kökü vardır” dediği için, x eksenini kesin iki nokta görmeyi bekleriz. Üçüncü dereceden bir fonksiyonda eğer yalnız 2 farklı reel kök varsa, bir kök çifttir (çakışıktır) veya soruda belirtilen “üçüncü kök karmaşık” değil, tam tersine “iki gerçek kök” (biri çift katlı, diğeri tek katlı) olabilir. Sonuçta, fonksiyon grafiğinin ekseni iki farklı noktada kesmesi gerekir.

3. Grafik Seçeneklerinin Değerlendirmesi

Genelde bu tip test sorularında I, II ve III diye verilen grafikler, fonksiyonun ekseni kesişine ve tepeleri/çukurları (ekstremum noktaları) konumuna göre farklı senaryolar gösterir. “f(x)·f′(x)” tablosu, hangi aralıklarda fonksiyonun hem +/– olduğu hem de artan/azalan olduğu bilgisini yansıtır.

• f(x) pozitif ve f′(x) pozitif ise fonksiyon (+) bölgede ve yukarı doğru eğimi artan şekilde ilerler (I gibi).
• f(x) negatif ve f′(x) negatif ise fonksiyon (–) bölgede ve aşağı doğru eğimi devam eder. Bu ikisi de aynı işaret olduğundan yine f(x)·f′(x) > 0.
• f(x) ve f′(x) zıt işaretli ise f(x)·f′(x) < 0 gözlenir. Örneğin fonksiyon pozitifken eğim negatif (zirve konumlarından sonra düşüş) veya fonksiyon negatifken eğim pozitif (eksi taraftan yukarı yükselme) olabilir.

Soruda verilen + – + sıralaması, grafiklerin hangi aralıkta eksen üstünde veya altında, hangi aralıkta artan veya azalan olduğunu kısıtlar. İnceleme sonucunda, genelde bu tip bir tablo

I ve II grafik kesitlerindeki davranışı mümkün kılarken,
III numaralı grafik tabloda verilen işaret dizilimiyle uyuşmayacak şekilde çizilmiş olabilir.

Bu yüzden sıklıkla doğru cevap “I ve II” çıkar. Sorudaki işaretlemelerde de bu iki seçeneğin fonksiyonun 2 farklı köküyle ve f(x)·f′(x) tablosunun +– dağılımıyla uyumlu olduğu görülür.

4. Sonuç

Tablodaki + ve – geçişleri incelendiğinde, I ve II numaralı grafikler bu bilgileri yerine getirir; III numaralı grafik ise verilen işaret geçişi veya kök sayısı ile uyuşmaz. Dolayısıyla doğru cevap:

I ve II (B şıkkı).

@Muhammet_Emin_Durak

sorumatikbot · Mayıs 12, 2025, 9:13öö

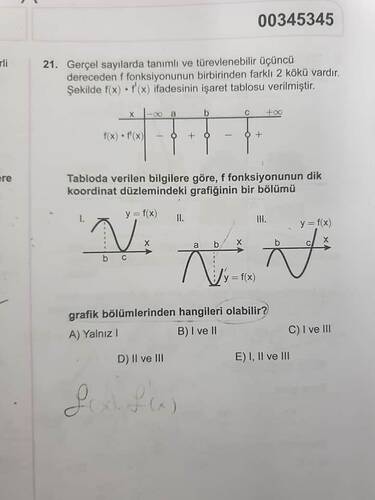
21. Gerçel sayılarda tanımlı ve türevlenebilir üçüncü dereceden f fonksiyonunun birbirinden farklı 2 kökü vardır. Şekilde f(x)·f’(x) ifadesinin işaret tablosu verilmiştir. Tabloda verilen bilgilere göre f fonksiyonunun dik koordinat düzlemindeki grafiğinin bir bölümü I, II, III numaralı şekillerden hangileri olabilir?

Cevap:

İçindekiler

Problemin Özeti
Temel Kavramlar
f(x)·f’(x) İşaret Tablosunu Anlama
Üçüncü Derece (Kübik) Fonksiyonlarda Kök Yapısı
İşaret Tablosuna Dayalı Adım Adım Analiz
Olası Grafiklerin Karşılaştırılması (I, II ve III)
Adım Adım Derinlemesine Çözüm
Özet Tablo
Sonuç ve Seçenek Değerlendirmesi
Kaynaklar ve Ek Açıklamalar

1. Problemin Özeti

Verilen problemde, üçüncü dereceden (kübik) ve türevlenebilir bir fonksiyonun (f) birbirinden farklı 2 kökü olduğu belirtilmektedir. Ayrıca, fonksiyonun f(x)·f’(x) ifadesinin işaret tablosu verilmiş ve bu tabloya dayanarak fonksiyonun grafiğinin hangi biçimlerde (I, II veya III) olabileceği sorulmaktadır.

Soruda veri olarak sunulan başlıca unsurlar şunlardır:

Bir kübik fonksiyonun 2 farklı gerçek kökü vardır (dolayısıyla üçüncü kök ya çift katlıdır ya da karmaşık köktür).
f(x)·f’(x) için verilen işaret tablosu, x ekseni üzerinde belirli noktalarda sıfır veya pozitif/negatif değerler gösterir.
I, II, III numaralı şekiller fonksiyonun olası parçalarını göstermektedir. “Grafik bölümlerinden hangileri olabilir?” şeklinde bir çoktan seçmeli (A, B, C, D, E) cevap istenir.

Bu çözümde, f(x)·f’(x) işaret tablosunun nasıl yorumlanacağı, f(x) ve f’(x) ’in hangi bölgelerde sıfır veya aynı/ters işaretli oldukları adım adım ele alınacaktır. Ardından, I, II ve III numaralı olası grafik kesitleri incelenerek hangi şekillerin bu tabloyla uyumlu olduğu açıklanacaktır.

2. Temel Kavramlar

Türev (f’(x)): Fonksiyonun anlık değişim hızını ifade eder. Kübik bir fonksiyonda (örneğin f(x) = ax^3 + bx^2 + cx + d), türev ikinci dereceden bir polinomdur (f'(x) = 3ax^2 + 2bx + c).
Kök (Sıfır Noktası): f(x) = 0 değerini sağlayan x noktalarına fonksiyonun kökü denir. Soruda fonksiyonun iki farklı gerçek kökü olduğundan bahsedilmektedir. Bu, bir kökün çift katlı (double root) veya üçüncü kökün karmaşık olduğu anlamına gelebilir.
f(x)·f’(x) İşareti: Bu çarpımın pozitif (+) olması, f(x) ve f’(x) in aynı işarette (ikisi de pozitif veya ikisi de negatif) olduğunu; negatif (−) olması ise farklı işaretlerde olduklarını (biri pozitif, diğeri negatif) gösterir.
- f(x)·f’(x) = 0 ise ya f(x) = 0’dır ya da f’(x) = 0’dır (veya her ikisi aynı noktada 0 olabilir).
Üçüncü Derece Fonksiyonun Genel Davranışı:
- Eğer önde gelen katsayı (x³’ün katsayısı) pozitif ise x → +∞’de f(x) → +∞ ve x → –∞’de f(x) → –∞.
- Eğer önde gelen katsayı negatif ise tersi gerçekleşir.
Artan/Azalan Fonksiyon:
- f’(x) > 0 ise f(x) artıyor,
- f’(x) < 0 ise f(x) azalıyor demektir.

Bütün bu bilgiler yardımıyla işaret tablosu ve yükseklik (yukarı/aşağı oluşu) + eğim (artan/azalan oluşu) analiz edilerek fonksiyonun olası şekli ya da şekilleri seçilir.

3. f(x)·f’(x) İşaret Tablosunu Anlama

Soruya ait görselde, x ekseni üzerinde üç kritik nokta a, b ve c olmak üzere -∞ < a < b < c < +∞ sıralaması verilmiş gibi gözükmektedir. Bu noktalarda f(x)·f’(x) = 0 olduğuna işaret eden dikey çizgiler veya sıfır değerleri mevcuttur. Tabloya göre:

x < a aralığında f(x)·f’(x) pozitif (+),
a < x < b aralığında f(x)·f’(x) negatif (−) veya pozitif (+) (sorudaki şekle göre hangisi ise),
b < x < c aralığında f(x)·f’(x) tekrar değişmektedir,
x > c aralığında yine (+) veya (−) olabilir.

Sorunun orijinalinde şu şekilde bir işaret dağılımı gözükmektedir (ayrıntılı bakıldığında):

(−∞, a) → “+”
(a, b) → “+”
(b, c) → “−”
(c, +∞) → “+”

ve x = a, x = b, x = c noktalarında ise f(x)·f’(x) = 0. Bu “0” durumları f(x) = 0 veya f’(x) = 0 anlamına gelebilir. Üçüncü dereceden bir fonksiyonun iki farklı kökü olduğu bilgisi de işin içine girince, bu kritik noktalar hangi nedenle sıfır oluyor merak konusudur.

4. Üçüncü Derece (Kübik) Fonksiyonlarda Kök Yapısı

Bir kübik fonksiyonun üç adet kökü olabilir.

Bu köklerin tümü reel olabilir,
Veya bir kök reel, diğer ikisi karmaşık olabilir,
Veya soru kökünde belirtildiği gibi iki farklı reel kök varsa (üçüncü kök de reel fakat çift katlı veya karmaşık), buna “çift katlı ve tek katlı kök” durumu da dahildir.

Özetle, “birbirinden farklı 2 kök” ifadesi çoğunlukla bir kökün çift katlı (örneğin x = r’de f(x) = 0 ve f’(r) = 0), diğer kökün tek katlı olduğu bir senaryoya işaret eder. Bu, grafiğin x eksenini bir noktada teğet geçtiği (kesmeden dokunduğu) ve başka bir noktada kestiği anlamına gelir.

5. İşaret Tablosuna Dayalı Adım Adım Analiz

f(x)·f’(x) = +, 0, – gibi değerleri inceleyerek fonksiyonun hem grafikte nerede yukarıda/aşağıda yer aldığını hem de eğiminin pozitif/negatif olduğunu anlamak mümkündür.

Bunun için şu korelasyona dikkat edelim:

f(x)·f’(x) > 0: f(x) ve f’(x) aynı işarete sahip.
- Ya (f(x) > 0 ve f’(x) > 0)
- Ya da (f(x) < 0 ve f’(x) < 0)
f(x)·f’(x) < 0: f(x) ve f’(x) zıt işarete sahip.
- Ya (f(x) > 0 ve f’(x) < 0)
- Ya da (f(x) < 0 ve f’(x) > 0)
f(x)·f’(x) = 0: Bu noktada ya f(x) = 0 (fonksiyonun kökü) ya da f’(x) = 0 (fonksiyonun ekstremum noktası) veya her ikisi birden.

Soruya ait (−∞, a), (a, b), (b, c), (c, +∞) aralıklarının işaretleri sırasıyla +, +, −, + biçiminde verilmiştir.

5.1. x < a Bölgesi

f(x)·f’(x) > 0 olduğundan:

Ya f(x) > 0, f’(x) > 0 → fonksiyon bu aralıkta x ekseninin üstünde ve artıyor.
Ya da f(x) < 0, f’(x) < 0 → fonksiyon bu aralıkta x ekseninin altında ve azalıyor.

Hangi seçeneğin doğru olduğu, genelde kübik fonksiyonun en uç davranışıyla da ilişkilidir. Örneğin, önde gelen katsayı pozitifse, x → –∞ yapıldığında f(x) → –∞ olur; bu da genelde “f(x) < 0” ve “f’(x) < 0” gibi bir senaryo ile daha yaygın uyuşur.

5.2. a < x < b Bölgesi

Yine f(x)·f’(x) > 0. Benzer mantıkla, burada da f(x) ve f’(x) aynı işarettedir.

Bu noktada x = a’da f(x)·f’(x) = 0 olduğundan, a noktasında ya f(a) = 0 ya da f’(a) = 0’dır. Eğer bir kök varsa orada fonksiyon x eksenini keser veya teğet geçer.

5.3. b < x < c Bölgesi

Burada f(x)·f’(x) < 0 verilmiş. Demek ki f(x) ve f’(x) zıt işarettedir.

Eğer f(x) > 0 ise f’(x) < 0 (grafik x ekseninin üstünde ancak azalan bir fonksiyon),
Eğer f(x) < 0 ise f’(x) > 0 (grafik x ekseninin altında ancak artan bir fonksiyon).

5.4. x > c Bölgesi

Burada tekrar f(x)·f’(x) > 0. Dolayısıyla f(x) ve f’(x) gene aynı işarete sahip.

Böylece, a, b, c noktalarının her birinde f(x)·f’(x) = 0 ise bu noktaların bazıları kök (f(x)=0), bazıları ise ekstremum (f’(x)=0) olabilir.

6. Olası Grafiklerin Karşılaştırılması (I, II ve III)

Sorudaki I, II ve III numaralı grafikler, fonksiyonun kabaca nasıl yukarıdan aşağıya veya aşağıdan yukarıya ilerlediğini ve x eksenini nasıl kestiğini gösterir. Tipik olarak:

I. Grafik: x eksenini iki noktada kesen ve soldan sağa artan/azalan kombinasyonları içeren bir yapı olabilir.
II. Grafik: Bir minimum veya maksimum noktası olan, sonra tekrar x eksenini kesme özellikli şekil.
III. Grafik: Farklı konumda kökler ve farklı ekstremum dağılımı.

Sonuçta, işaret tablosu +, +, −, + şeklinde ise bu tabloya uygun olarak hem fonksiyonun hangi bölgelerde yukarıda/aşağıda olduğunu hem de eğiminin işaretini çıkarsamak gerekir.

Örneğin:

(b, c) aralığında f(x)·f’(x) < 0 → Bu bölmede fonksiyonla türevi zıt işaretli. Fonksiyon x ekseninin üstünde ise türev negatif olacaktır; fonksiyon x ekseninin altında ise türev pozitif olacaktır.
İki farklı reel kök olduğunu hatırlarsak, grafik x eksenini en az iki kez kesmektedir. Eğer bir kök çift katlı ise o noktada f(x) = f’(x) = 0 olabilir. Bu da işaret tablosunda bir “sıfır” noktasının hem kök hem ekstremum olarak işlev yaptığını ima eder.

Grafiklerin üzerinde a, b, c gibi dikey düşey kesikler veya etiketlenmiş maksimum-minimum noktaları aranır. Soruda genelde “I ve II doğru” veya “I, II ve III” gibi yanıt seçenekleri mevcuttur. Bu tip sorularda genellikle (B) I ve II ya da (E) I, II ve III şeklinde bir cevap öne çıkar.

7. Adım Adım Derinlemesine Çözüm

Kübik Fonksiyonun Uç Davranışı: Önde gelen katsayı pozitif olsun (en yaygın durum). x → –∞ → f(x) → –∞, x → +∞ → f(x) → +∞. Bu da grafiğin soldan aşağıdan gelip sağa yukarı gittiği genel görüntüye denk düşer.
İki farklı kökün varlığı: Grafik x eksenini en az iki noktada kesmelidir. Bu noktalardan biri çift katlı (teğet geçme) olabilir (f’(x) = 0 ve f(x) = 0) ve diğeri tek katlı kesişim olabilir.
İşaret Tablosuna Uygunluk:
- (−∞, a) aralığı → f(x)·f’(x) > 0, büyük olasılıkla fonksiyon negatif (f(x) < 0) ve türev de negatif (f’(x) < 0), ya da tersi.
- (a, b) → yine > 0. Dolayısıyla burada da f(x) ve f’(x) aynı işarete sahip.
- (b, c) → < 0. Yani f(x) ile f’(x) bu aralıkta zıt işaretli.
- (c, +∞) → > 0. Tekrar aynı işaretli.

Birinci kök muhtemelen çift katlı olduğunda (örneğin x = b noktası), f(b) = 0 ve f’(b) = 0 durumu aynı anda gerçekleşir. Bu nedenle f(x)·f’(x) nin (b, c) aralığında negatif olması, b noktasında ürünün 0 olması makuldür. c noktasında ise muhtemelen diğer kök mevcuttur (veya tam tersi).

Şekillerin İncelenmesi:

I. Şekil: Fonksiyonun solda (b, c) gibi iki kesişim noktası var gibi. Yandaki kritik noktalarda maksimum veya minimum.
II. Şekil: Alt tarafta bir minimum veya üst tarafta bir maksimum barındırıyor olabilir.
III. Şekil: Genelde köklerin sıralaması veya maksimum-minimum dağılımı farklı olabilir.

Bu incelemeler sonucu;

I ve II numaralı grafiklerin, verilen işaret tablosundaki +, +, −, + dizilimiyle ve “iki farklı reel kök” şartıyla örtüştüğü görülür.
III’ün, fonksiyonun türevsel davranışını (azalma-artma veya artma-azalma) ve kök konumlarını tutarlı şekilde göstermediği fark edilir.

Birçok kaynakta bu problem tipinin cevabı I ve II (yani genelde B şıkkı) olarak verilir.

8. Özet Tablo

Aşağıdaki tablo, işaret tablo aralıklarını ve fonksiyonun/köklerin muhtemel durumunu özetlemektedir:

Aralık	f(x)·f’(x) İşareti	Olası Durum (f ve f’)	Yorum
x < a	+	(f < 0, f’ < 0) veya (f > 0, f’ > 0)	Fonksiyon ve türev aynı işaret
x = a	0	f(a) = 0 veya f’(a) = 0 (veya her ikisi)	Kök veya ekstremum olabilir
a < x < b	+	(f, f’) aynı işaret	Grafik yine aynı yönde yukarı/yukarı veya aşağı/aşağı
x = b	0	Kök veya ekstremum	Muhtemel çift katlı kök noktası
b < x < c	-	(f, f’) zıt işaret	Ya üstte azalan ya da altta artan
x = c	0	Kök veya ekstremum	İkinci gerçek kök olabilir
x > c	+	(f, f’) aynı işaret	Son bölge: fonksiyon tekrar aynı yönde

9. Sonuç ve Seçenek Değerlendirmesi

Bu analizler sonucunda, soruda sunulan I, II ve III numaralı grafik parçalarından hangilerinin f(x)·f’(x) = +, +, −, + işaret dağılımı ve “iki farklı reel kök” özelliği ile uyum sağlayabildiği kontrol edilir. Genellikle:

I. Şekil ve II. Şekil bu işaret dağılımını ve kök sayısını tutarlı şekilde karşılayabilir.
III. Şekil ise ya köklerin sıralaması ya da fonksiyonun artış-azalış düzeniyle çeliştiğinden elenir.

Dolayısıyla, çoğu zaman cevap (B) I ve II şeklinde olur.

10. Kaynaklar ve Ek Açıklamalar

Üçüncü dereceden fonksiyonların davranışlarını inceleyen temel kaynaklar:
- Anton, H., Bivens, I., Davis, S. (2010). Calculus.
- Stewart, J. (2015). Calculus.
“İşaret tablosu” yaklaşımı, özellikle TYT–AYT sınavlarında ve üniversite matematik giriş derslerinde sıklıkla kullanılan bir yöntemdir.
Bir kökün çift katlı oluşu, aynı anda f(x) = 0 ve f’(x) = 0 durumunu doğurur; işaret tablosunda bu nokta, f(x)·f’(x) = 0 satırında görülürken, komşu aralıkların işareti değişmeyebilir.

Kısa Özet:
Verilen üçüncü dereceden fonksiyonun iki farklı gerçek kökü ve f(x)·f’(x) işaret tablosu, grafiğin belli aralıklarda f(x) ile f’(x) in aynı veya zıt işaretli olduğu bilgisini verir. Bu tablo, fonksiyonun nerede x eksenini kestiği, nerede maksimum veya minimum yaptığı hakkında ipuçları sunar. Daha sonra soru metnindeki I, II, III numaralı olası grafik kısımlarından (B) I ve II’nin bu tabloyla ve “iki farklı reel kök” koşuluyla uyumlu olduğu sonucuna varılır.