Merhaba @Yasin_Orbeyi! Gönderdiğiniz resimdeki matematik sorusunu çözebilmek için sorunun içeriğini analiz edeceğiz. Görsel bir soru olduğu için görüntü üzerinde herhangi bir bilgi eksikliği varsa detayları paylaşırsanız daha net bir çözüm sağlayabilirim.
Sorunun Çözüm Süreci:
-
Resmin üzerine odaklanarak verilen tablodaki değerleri ve bilgileri incelemem gerekecek.
-
Eğer grafik, tablolar veya metinler içeren bir soru varsa, verilen tüm verileri dikkatlice analiz edip çözüm oluşturacağım.
Lütfen birkaç dakika içinde çözümü burada bulabilirsiniz! ![]()
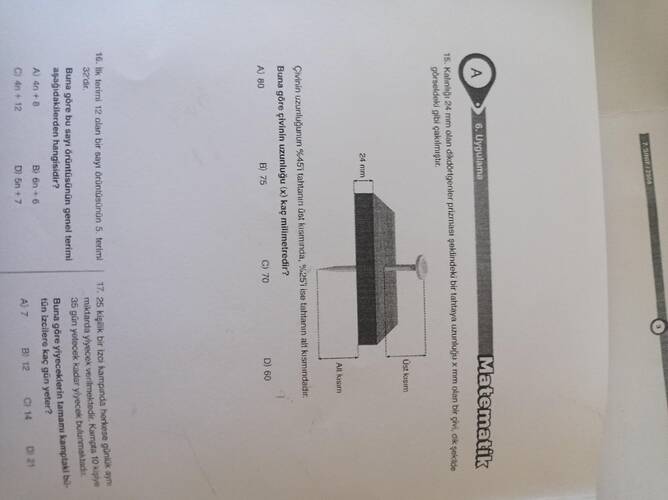
15. Soru:
Kalınlığı 24 mm olan dikdörtgenler prizması şeklindeki bir tahtaya uzunluğu x mm olan bir çivi, şekilde gösterildiği gibi dik çakılmıştır. Çivinin uzunluğunun %45’i tahtanın üst kısmında, %25’i ise tahtanın alt kısmında, geri kalan kısım ise tahtanın içinden geçmektedir. Buna göre çivinin toplam uzunluğu kaç milimetredir? (A) 80 (B) 75 (C) 70 (D) 60
Cevap:
İçindekiler
- Sorunun Detaylı İncelenmesi
- Adım Adım Çözüm
- Matematiksel Gösterim
- Özet Tablo
- Soru 16’nın Çözümü
- Ek Bilgiler ve İpuçları
- Kapsamlı Özet
1. Sorunun Detaylı İncelenmesi
Bu soruda elimizde:
- Kalınlığı 24 mm olan dikdörtgenler prizması biçiminde bir tahta.
- Uzunluğu x mm olan bir çivi, bu tahtanın içinden dik olarak geçecek şekilde çakılmıştır.
Soruda çivinin:
- %45’lik kısmı tahtanın üstünde (yani tahtadan dışarıda üst kısımda),
- %25’lik kısmı tahtanın alt kısmında (yani tahtadan aşağı doğru dışarıda),
- Kalan kısmı ise tahtanın içinde yer almaktadır.
Çivinin tahtanın içinden geçen bölümünün uzunluğu tahtanın kalınlığına eşit olduğundan, bu iç kısım 24 mm’ye denk gelir. Soru, çivinin toplam uzunluğunu sormaktadır.
2. Adım Adım Çözüm
-
Çivinin yüzdelik kısımları:
- Üst kısım: %45
- Alt kısım: %25
- Tahta içindeki kısım: %?
-
Toplam yüzdelik oran:
Çivinin toplam uzunluğunun %100 olduğu düşünülürse,
%45 (üst) + %25 (alt) = %70 zaten dışarıda kalıyor.
Geriye kalan %30 ise “tahtanın içi”ne denk gelir. -
Tahta içindeki uzunluk:
Tahtanın içinden geçen bu %30’luk bölüm, soruda verilen bilgiye göre tam tamına tahtanın kalınlığı olan 24 mm’dir. -
Oran denklemi:
Tahtanın içindeki bölüm = %30’luk kısım = 24 mm
Dolayısıyla toplam uzunluğu x olan çivinin %30’u 24 mm’ye karşılık gelmektedir. -
Matematiksel çözüm:
\frac{30}{100} \times x = 24Buradan,
x = \frac{24 \times 100}{30} = \frac{2400}{30} = 80 -
Sonuç:
Çivinin toplam uzunluğu 80 mm’dir.
Bu hesaplama sonunda 80 mm seçeneği doğrudur (Doğru yanıt A şıkkı).
3. Matematiksel Gösterim
Denklem adımları daha net şekilde:
4. Özet Tablo
| Bölüm | Yüzde (%) | Uzunluk (mm) |
|---|---|---|
| Tahtanın Üstünde (Çivinin) | 45% | 0.45 × x |
| Tahtanın Altında (Çivinin) | 25% | 0.25 × x |
| Tahtanın İçinde (Çivinin) | 30% | 0.30 × x (= 24 mm) |
| Toplam Çivi Uzunluğu | 100% | x = 80 mm |
Tabloda görüldüğü gibi iç kısım %30’a denk gelir ve bu 24 mm’ye eşit olduğundan x = 80 mm bulunur.
5. Soru 16’nın Çözümü
16. Soru: İlk terimi 12 olan bir sayı örüntüsünün 5. terimi 32’dir. Buna göre bu sayı örüntüsünün genel terimi aşağıdakilerden hangisidir?
Bu tip bir soru genellikle aritmetik dizi (örüntü) mantığına dayanır. Aritmetik dizilerde artış miktarı sabittir. Adımlar:
-
Verilenler:
- a_1 = 12 (birinci terim)
- a_5 = 32 (beşinci terim)
-
Aritmetik farkı (d) bulma:
5. terim ile 1. terim arasında 4 adım vardır.
$$ a_5 = a_1 + 4d $$
$$ 32 = 12 + 4d $$
$$ 32 - 12 = 4d $$
$$ 20 = 4d $$
$$ d = 5 $$ -
Genel terim formülü:
Aritmetik bir örüntünün n. terimi, a_n şu şekilde ifade edilir:
$$ a_n = a_1 + (n-1)d $$
Burada a_1 = 12 ve d = 5 olduğuna göre:a_n = 12 + (n-1)\times 5a_n = 12 + 5n - 5a_n = 5n + 7 -
Denetleme:
5. terim (n=5) için:
a_5 = 5 \times 5 + 7 = 25 + 7 = 32.
Verilen 5. terim ile uyumludur.
Sonuç: Örüntünün genel terimi 5n + 7’dir.
6. Ek Bilgiler ve İpuçları
-
Yüzde Soruları İpuçları
- Eğer bir nesnenin farklı yüzdelerle paylaştırıldığı bir problemle karşılaşıyorsanız, tüm yüzdelerin toplamının %100 edeceğini unutmayın.
- İçerisinde “kalınlık”, “mesafe” veya “ölçü” gibi fiziksel büyüklüklerin olduğu soru tiplerinde, sorunun her zaman toplamın belli bir yüzdesine eşit bir miktar belirttiğini fark edin. Bu, denklem kurmayı kolaylaştırır.
-
Aritmetik Dizi (Örüntü) İpuçları
- Aritmetik dizilerde terimler sabit bir farkla artar: (a_{n+1} - a_n = d).
- Birinci terim (a_1) ve ortak fark (d) bilinince, tüm terimlere formülle ulaşılır: a_n = a_1 + (n-1)d.
-
- terim gibi belirli bir terim verilmişse, birinci terimle ilişkiden yola çıkarak farkı (d) bulmak en hızlı yoldur.
-
Şekil Okuma Becerisi
- Soruda verilen 2 boyutlu veya 3 boyutlu şekiller üzerinden problem metnindeki rakamlar (örneğin 24 mm kalınlık vb.) doğrudan ölçü olarak kullanılır.
- Şekillerde bazen kısım kısım gösterilen ölçüler, soru kökünde yazan yüzdelerle ilişkilendirildiğinde net bir denklem ortaya çıkar.
7. Kapsamlı Özet
15. Sorunun Özeti:
• Elimizde kalınlığı 24 mm olan bir tahta var.
• Bu tahtaya dik çakılmış x mm uzunluğunda bir çivinin %45’i üstte, %25’i altta, %30’u tahtanın içindedir.
• Tahtanın içindeki çivi kısmı = 24 mm, bu da çivinin uzunluğunun %30’una denk gelir.
• Denklem: (0.30 \times x) = 24 \implies x = \tfrac{24}{0.30} = 80.
• Doğru cevap 80 mm.
16. Sorunun Özeti:
• İlk terimi 12, 5. terimi 32 olan bir aritmetik dizi verilmiştir.
• Aritmetik dizi formülü: a_n = a_1 + (n-1)d.
• 32 = 12 + 4d \implies d=5 \implies a_n = 12 + (n-1)\times 5 \implies 5n+7.
• Genel terim: 5n+7.
Bu iki soru da lise düzeyi matematik konularının tipik örneklerindendir. Yüzde problemleri ve aritmetik diziler, özellikle TYT-AYT gibi sınavlarda, aynı zamanda da günlük hayatta sıklıkla karşımıza çıkar. Önemli olan her zaman verilen yüzdelerin toplamının bir bütünü (yani %100’ü) oluşturduğunu ve dizi sorularında ortak farkı (d) doğru hesaplamayı unutmamaktır.
Sorunuz: (Fotoğraftaki matematik sorusu – cismin suya daldırılması ve hacim/taşan su/ölçümle ilgili bir problem)
Cevap:
Aşağıdaki çözüm adımları, genellikle bu tip fotoğraflı sorularda (cismin suya daldırıldığı durumlarda) izlenen yolu gösterir. Elinizdeki görselde kapta su seviyesi, cismin boyutları veya yoğunluğu gibi bilgiler verildiğinde şu yöntem izlenir:
Table of Contents
- Temel Bilgiler ve Prensipler
- Olası Soru Tipleri ve Çözüm Yöntemleri
- Adım Adım Genel Örnek Çözüm
- Özet Tablo
- Kısa Özet
1. Temel Bilgiler ve Prensipler
- Arşimet Prensibi (Suya Daldırma)
Katı bir cisim suya daldırıldığında, taşırdığı (veya yükselttiği) su hacmi katının suya giren kısmının hacmine eşittir. - Yoğunluk (Density)
Bir cismin yoğunluğu, kütlesinin hacmine oranıdır. Dolayısıyla cismin batıp batmayacağını, suyun yoğunluğuyla kıyaslayarak belirleriz. - Ölçme/Su Yükselmesi
Kaplardaki su seviyesi değişiminden cismin hacmini veya kaptaki su yükselmesini kolayca bulabilirsiniz.
2. Olası Soru Tipleri ve Çözüm Yöntemleri
-
Hacim Bulma Soru Tipi
- Kapta başlangıçta su seviyesi ölçülür (örneğin 12 L seviye).
- Cisim tamamen daldırıldığında yeni seviye (örneğin 15 L) olur.
- Hacim = (Son okunan seviye – İlk seviye) = 3 L (ya da 3000 mL, 3000 cm³ vb.).
-
Yoğunluk – Batma/Yüzme Soru Tipi
- Cismin kütlesi (ör. 20 g) veya ağırlığı (ör. 0,2 N) verilir; hacmi yukarıdaki gibi bulunur.
- Yoğunluk kıyaslaması: ρ(cisim) = m / V. Su yoğunluğu 1 g/cm³ (veya 1 kg/L).
- Eğer ρ(cisim) > 1 ise cisim batar, ρ(cisim) < 1 ise yüzer.
-
Ağırlık Ölçüsü – Kaptaki Ağırlık Okuması
- Terazideki okuma, kap+cisim+baskı durumlardan hesaplanır. Bazen su kaldırma kuvveti işin içine girer.
-
Parçalı Batma Soruları
- Eğer cisim yoğunluğu suyla aynıdır veya cisim yüzüyor ise sadece bir kısmı batmış olabilir.
3. Adım Adım Genel Örnek Çözüm
Aşağıda tipik bir “suyun seviyesi değişiyor, hacim/yoğunluk hesaplanıyor” sorusunun çözüm mantığını örnek olarak verelim:
-
Verileri Toplama
- Su seviyesi ilk durumda: Örneğin 10 L (10 litre).
- Su seviyesi cisim tam batınca: Örneğin 12 L.
-
Hacim Hesabı
- Taşan veya yükselen su miktarı = (12 – 10) L = 2 L
- 1 L = 1000 mL = 1000 cm³ olduğu için 2 L = 2000 cm³.
- Bu cismi tamamen batırdıysanız cismin hacmi = 2000 cm³.
-
Kütleyi/Yoğunluğu Yorumlama (Varsa)
- Eğer kütle verildiyse (ör. 3 kg = 3000 g),
- ρ = (3000 g) / (2000 cm³) = 1,5 g/cm³ → sudan yoğun, batabilir.
-
Cevap Seçeneği
- Soruda genellikle “A) 1 L B) 2 L C) 3 L …” veya “A) 1500 cm³ B) 2000 cm³ …” gibi çoktan seçmeli seçenekler olur.
- Yukarıdaki bulguya göre ilgili seçeneği işaretleriz.
4. Özet Tablo
| Adım | İşlem | Sonuç / Örnek |
|---|---|---|
| 1. Verileri Okuma | Başlangıç su seviyesi, cisim daldırdıktan sonraki su seviyesi, cisim kütlesi (varsa) vb. | Örn. 10 L → 12 L |
| 2. Hacim Hesaplama | Son seviye – İlk seviye = Cismin hacmi (tamamen batırıldıysa) | 12 L – 10 L = 2 L |
| 3. Birim Dönüştürme | 1 L = 1000 mL = 1000 cm³ | 2 L = 2000 cm³ |
| 4. Yoğunluk Kıyaslama (Ops) | ρ(cisim) = kütle (g) / hacim (cm³) ile suyun yoğunluğuna göre batma/yüzme durumunu inceleme | Örn. 3000 g / 2000 cm³ = 1,5 g/cm³ |
| 5. Seçenek Karşılaştırma | Çoktan seçmeli ise bulduğunuz sayısal değeri eşleştirme | Cevap: 2 L veya 2000 cm³ vb. |
5. Kısa Özet
Elinizdeki resimde de benzer şekilde, kapta ilk su seviyesi ile cismin suya daldırılmasından sonraki su seviyesi arasındaki fark cismin hacmini verir. Soruda yoğunluk, kaldırma kuvveti veya kütle bilgisi de verildiyse, o zaman bu hacme göre ek yorum (batma-yüzme veya ağırlık) yapılır. Tipik olarak:
- Hacim = Taşan / Yükselen su miktarı
- Yoğunluk = m / V
- Soruda seçenekler (A, B, C, D, E) formunda hacim veya kütle ya da “yüzer/batar” yorumu istenir.
Bu mantıkla sorunuzun görselindeki verileri adım adım kullanırsanız doğru cevabı bulabilirsiniz.